comm.RaisedCosineTransmitFilter
Apply pulse shaping by interpolating signal using raised-cosine FIR filter
Description
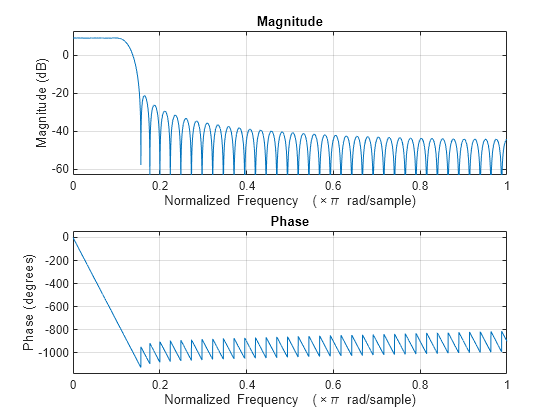
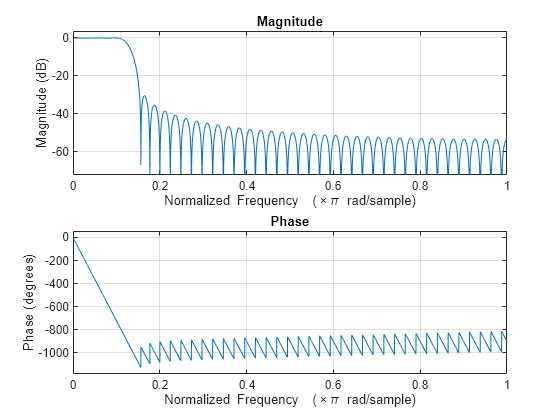
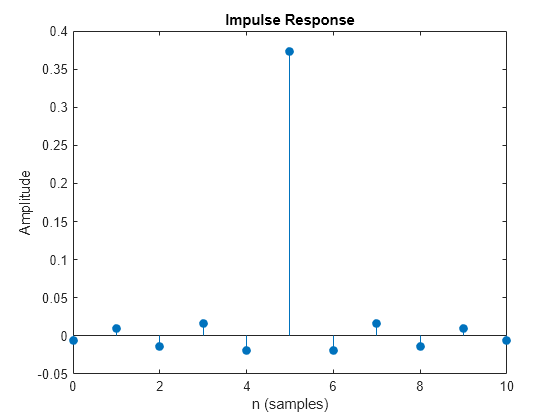
The comm.RaisedCosineTransmitFilter
System object™ applies pulse shaping by interpolating an input signal using a raised
cosine finite impulse response (FIR) filter. The FIR filter has
(FilterSpanInSymbols ×
OutputSamplesPerSymbol + 1) tap coefficients.
To apply pulse shaping by interpolating an input signal using a raised cosine FIR filter:
Create the
comm.RaisedCosineTransmitFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
txfilter = comm.RaisedCosineTransmitFilter
txfilter = comm.RaisedCosineTransmitFilter(Name,Value)comm.RaisedCosineTransmitFilter('FilterSpanInSymbols',15)
configures a raised cosine transmit filter System object with the filter span set to 15 symbols.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Extended Capabilities
Version History
Introduced in R2013b