Ideal Rectangular Pulse Filter
Shape input signal using ideal rectangular pulses
Libraries:
Communications Toolbox /
Comm Filters
Description
The Ideal Rectangular Pulse Filter block upsamples and shapes the input signal using rectangular pulses. After replicating input samples, the block can also normalize the output signal and apply a linear amplitude gain.
Examples
Apply ideal rectangular filtering to a ramp signal.
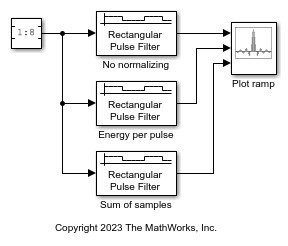
The cm_ideal_rect_pulse_filter model plots a ramp signal with various normalization methods applied. The model includes three Ideal Rectangular Pulse Filter blocks configured with Pulse length (number of samples) set to 4 and Pulse delay (number of samples) set to 3 to filter a ramp input signal, and an Array Plot block with default settings to display one frame of the output signals.
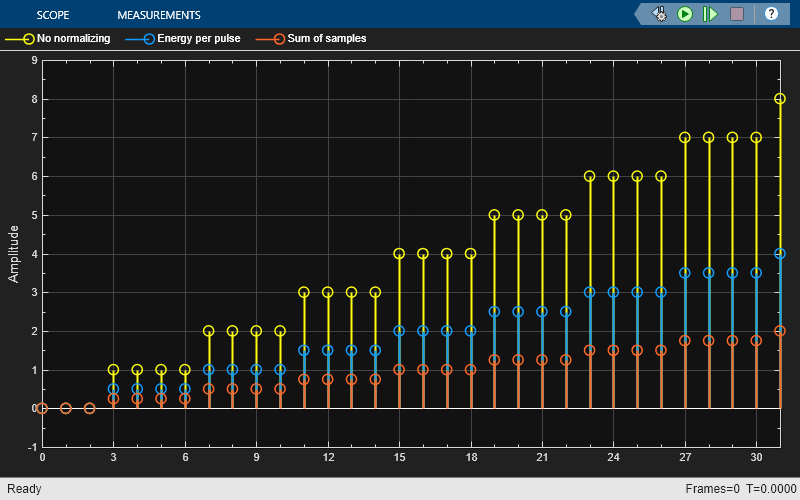
Run the model with Linear amplitude gain of the filters set to 1. The first three samples are zero because the filter blocks have pulse delay set to 3.
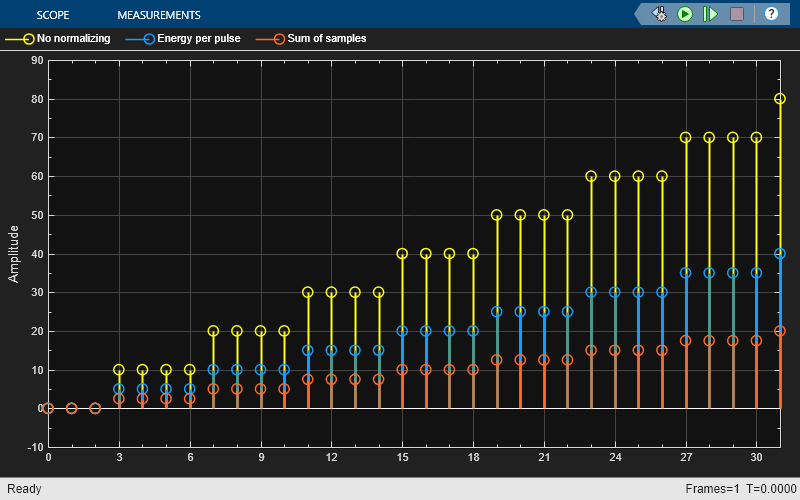
Run the model with Linear amplitude gain of filters set to 10.
Ports
Input
Input signal, specified as a scalar, column vector, or Ki-by-N matrix. Ki is the number of input samples per signal channel, and N is the number of signal channels.
Data Types: double | single | fixed point
Output
Output signal, returned as a scalar, column vector, or matrix. The block filters each channel over time and generates a Ko-by-N output matrix. The output signal is the same data type as the input signal.
Ko = Ki × L.
N is the number of signal channels.
Ki is the number of input samples per signal channel.
L is the value you specify in the Pulse length (number of samples) parameter.
Data Types: double | single | fixed point
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
Pulse length in samples, specified as a positive integer. The block replicates each input sample L times, where L is the pulse length that you specify in samples.
Pulse delay in samples, specified as a nonnegative integer. If this parameter is nonzero, then the block outputs that number of zeros at the beginning of the simulation, before starting to replicate any of the input values.
Input processing control, specified as one of these options:
Columns as channels (frame based)— The block treats each column of the input as a separate channel.Elements as channels (sample based)— The block treats each element of the input as a separate channel.
Block processing rate for input signal upsampling and filtering, specified as one of these options:
Enforce single-rate processing— When you select this option, the block maintains the input sample rate and processes the signal by increasing the output frame size by a factor of N.Allow multirate processing— When you select this option, the block processes the signal such that the output sample rate is N times faster than the input sample rate.
Dependencies
To use Enforce single-rate processing, you must set
Input processing to Columns as channels
(frame based).
Select this parameter to scale the set of replicated values before applying the linear amplitude gain.
Normalization method, specified as Sum of samples or
Energy per pulse. This parameter assigns the
quantity that the block considers when scaling the set of replicated values.
For more information, see Normalization Methods.
Dependencies
This parameter appears when you select Normalize output signal.
Linear gain, specified as a positive scalar. The block scales the output signal by the linear gain value that you specify. For more information, see Normalization Methods.
Data Types
Select the rounding mode for fixed-point operations. The block uses
rounding mode when the result of a fixed-point calculation does not map
exactly to a number representable by the data type. The filter coefficients
do not obey this parameter; they always round to
Nearest. For more information, see Rounding Modes
or Rounding Mode: Simplest (Fixed-Point Designer).
Select the overflow mode for fixed-point operations. The filter coefficients do not obey this parameter; they are always saturated.
Specify the word length and the fraction length of the filter coefficients (numerator and denominator).
When you select Inherit: Same word length as input, the word
length of the filter coefficients match that of the input to the block. In
this mode, the fraction length of the coefficients is automatically set to
the binary-point-only scaling that provides you with the best precision
possible given the value and word length of the coefficients.
For more information and illustrations depicting the use of the coefficient data types in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block.
The filter coefficients do not obey the Rounding
mode and the Saturate
on integer overflow parameters; they are always saturated
and rounded to Nearest.
For information about specifying data types, see Data Type Assistant.
Specify the product output word and fraction lengths.
When you select
Inherit: Inherit via internal rule, the block inherits the data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.When you select
Inherit: Same as input, these characteristics match those of the input to the block.
For more information and illustrations depicting the use of the product output data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) and Multiplication Data Types.
For information about specifying data types, see Data Type Assistant.
Specify the accumulator word and fraction lengths.
When you select
Inherit via internal rule, the block inherits the data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as product output, these characteristics match those of the product output.
For more information and illustrations depicting the use of the accumulator output data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) and Multiplication Data Types.
For information about specifying data types, see Data Type Assistant.
Specify the output word and fraction lengths.
When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as accumulator, these characteristics match those of the accumulator.When you select
Inherit: Same as product output, these characteristics match those of the product output.
For information about specifying data types, see Data Type Assistant.
Select this parameter to prevent the fixed-point tools from overriding the data types that you specify in the block dialog box. For more information, see the Fixed-Point Tool (Fixed-Point Designer).
Block Characteristics
More About
The Data Type Assistant helps you set data
attributes. To use the Data Type Assistant, click ![]() . For more information, see Specify Data Types Using Data Type Assistant (Simulink).
. For more information, see Specify Data Types Using Data Type Assistant (Simulink).
Algorithms
When you set the Rate
options parameter to Enforce single-rate
processing, the input and output of the block have the same sample
rate. To generate the output while maintaining the input sample rate, the block
resamples the data in each column of the input such that the frame size of the
output (MOut) is L
times larger than that of the input (MO =
MI×L), where
L is the Pulse length
(number of samples) parameter value.
When you set the Rate
options parameter to Allow multirate
processing, the input and output of the block are the same size.
However, the sample rate of the output is L times faster than
that of the input and the output sample time is 1 / L times the
input sample time, where L is the Pulse length
(number of samples) parameter value. When the block is in multirate
processing mode, you must also specify a value for the Input
processing parameter.
When you set the Input processing parameter to
Elements as channels (sample based), the block treats an M-by-N matrix input as (M×N) independent channels, and processes each channel over time. The output sample period, TS_Out, is L times shorter than the input sample period (TS_Out = TS_In / L), while the input and output sizes remain identical.When you set the Input processing parameter to
Columns as channels (frame based), the block treats an MIn-by-N matrix input as N independent channels. The block processes each column of the input over time by keeping the frame size constant (MIn=MOut), while making the output frame period, TF_Out, L times shorter than the input frame period (TF_Out = TF_In / L).
You configure the normalization behavior of the block by using the Normalize output signal and Linear amplitude gain parameters.
If you clear Normalize output signal, then the block multiplies the set of replicated values by the Linear amplitude gain parameter. This parameter must be a scalar.
If you select Normalize output signal, then the Normalization method parameter appears. The block scales the set of replicated values so that one of these conditions is true:
When you set the Normalization method parameter to
Sum of samples, the sum of the samples in each pulse equals the original input value that the block replicated. Effectively, the block uses a rectangular pulse with amplitude of (1 / L), where L is the pulse length.When you set the Normalization method parameter to
Energy per pulse, the sum of the squared samples in each pulse equals the square of the input value. Effectively, the block uses a rectangular pulse with amplitude of (1 / √L), where L is the pulse length.
After the block applies the scaling specified in the Normalization method parameter, it multiplies the scaled signal by the constant scalar value specified in the Linear amplitude gain parameter.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)