Interconnecting Linear Models

Arithmetic Operations for Interconnecting Models

You can perform arithmetic on LTI models, such as addition, multiplication, or concatenation. Addition performs a parallel interconnection. For example, typing

tf(1,[1 0]) + tf([1 1],[1 2])   % 1/s + (s+1)/(s+2)

produces this transfer function.

Transfer function:
s^2 + 2 s + 2
-------------
  s^2 + 2 s

Multiplication performs a series interconnection. For example, typing

2 * tf(1,[1 0])*tf([1 1],[1 2])   % 2*1/s*(s+1)/(s+2)

produces this cascaded transfer function.

Transfer function:
2 s + 2
---------
s^2 + 2 s

If the operands are models of different types, the resulting model type is determined by precedence rules; see Rules That Determine Model Type for more information.

For more information about model arithmetic functions, see Catalog of Model Interconnections.

You can also use the series and parallel functions as substitutes for multiplication and addition, respectively.

Equivalent Ways to Interconnect Systems

Operator	Function	Resulting Transfer Function
sys1 + sys2	parallel(sys1,sys2)	Systems in parallel
sys1 - sys2	parallel(sys1,-sys2)	Systems in parallel
sys1 * sys2	series(sys2,sys1)	Cascaded systems

Feedback Interconnections

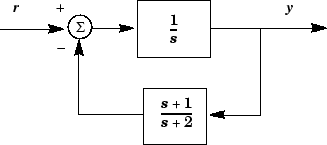
You can use the feedback and lft functions to derive closed-loop models. For example,

sys_f = feedback(tf(1,[1 0]), tf([1 1],[1 2])

computes the closed-loop transfer function from r to y for the feedback loop shown below. The result is

Transfer function:
    s + 2
-------------
s^2 + 3 s + 1

This figure shows the interconnected system in block diagram format.

Feedback Interconnection

You can use the lft function to create more complicated feedback structures. This function constructs the linear fractional transformation of two systems. See the reference page for more information.