Frequency Response of a MIMO System
This example shows how to examine the frequency response of a multi-input, multi-output (MIMO) system in two ways: by computing the frequency response, and by computing the singular values.
Calculate the frequency response of a MIMO model and examine the size of the output.
H = rss(2,2,2); H.InputName = 'Control'; H.OutputName = 'Temperature'; [mag,phase,w] = bode(H); size(mag)
ans = 1×3
2 2 89
The first and second dimension of the data array mag are the number of outputs and inputs of H. The third dimension is the number of points in the frequency vector w. (The bode command determines this number automatically if you do not supply a frequency vector.) Thus, mag(i,j,:) is the frequency response from the j th input of H to the i th output, in absolute units. The phase data array phase takes the same form as mag.
Plot the frequency response of each input/output pair in H.
bode(H)

bode plots the magnitude and the phase of the frequency response of each input/output pair in H. (Because rss generates a random state-space model, you might see different responses from those pictured.) The first column of plots shows the response from the first input, Control(1), to each output. The second column shows the response from the second input, Control(2), to each output.
Plot the singular values of H as a function of frequency.
sigma(H)
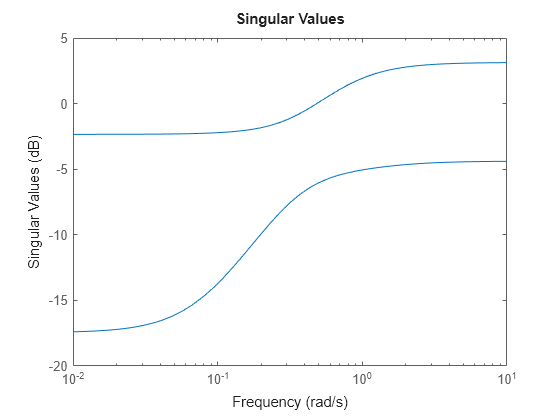
sigma plots the singular values of the MIMO system H as a function of frequency. The maximum singular value at a particular frequency is the maximum gain of the system over all linear combinations of inputs at that frequency. Singular values can provide a better indication of the overall response, stability, and conditioning of a MIMO system than a channel-by-channel Bode plot.
Calculate the singular values of H between 0.1 and 10 rad/s.
[sv,w] = sigma(H,{0.1,10});When you call sigma with output arguments, the command returns the singular values in the data array sv. The cell array input {0.1,10} tells sigma to calculate the singular values at a grid of frequencies between 0.1 and 10 rad/s. sigma returns these frequencies in the vector w. Each row of sv contains the singular values of H at the frequencies of w.
See Also
bode | bodeplot | sigma | sigmaplot