La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

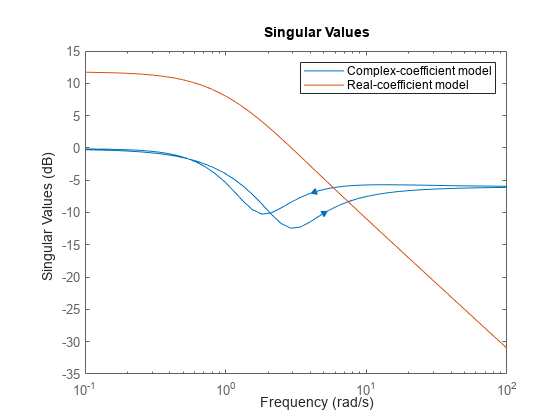
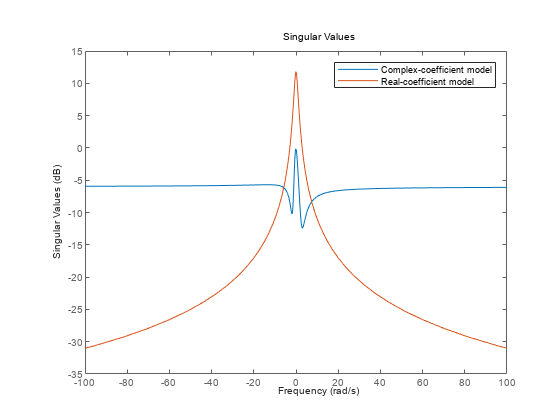
sigma

Valores singulares de la respuesta en frecuencia de un sistema dinámico

Sintaxis

[sv,wout] = sigma(sys)

[sv,wout] = sigma(sys,w)

sv = sigma(sys,w,type)

sigma(___)

Descripción

[sv,wout] = sigma(sys) devuelve los valores singulares sv de la respuesta en frecuencia del modelo de sistema dinámico sys en cada frecuencia del vector wout. La función determina automáticamente frecuencias para representar en función de la dinámica del sistema.

[sv,wout] = sigma(sys,w) devuelve valores singulares en las frecuencias especificadas por w. Puede especificar un rango de frecuencia o un vector de frecuencias.

sv = sigma(sys,w,type) devuelve valores singulares modificados del tipo especificado. Puede usar esta sintaxis solo para sistemas con el mismo número de entradas y salidas.

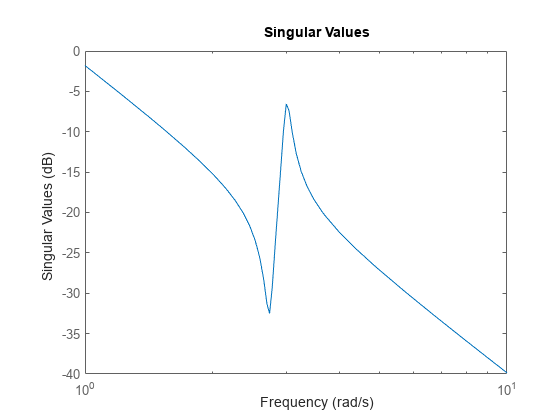
sigma(___) representa los valores singulares de la respuesta en frecuencia de sys con opciones de representación predeterminadas para todas las combinaciones de argumentos de entrada anteriores. Si sys es un modelo de única entrada y única salida (SISO), la gráfica de valores singulares es entonces similar a su respuesta de la magnitud de Bode. Para ver más opciones de personalización de gráficas, utilice sigmaplot.

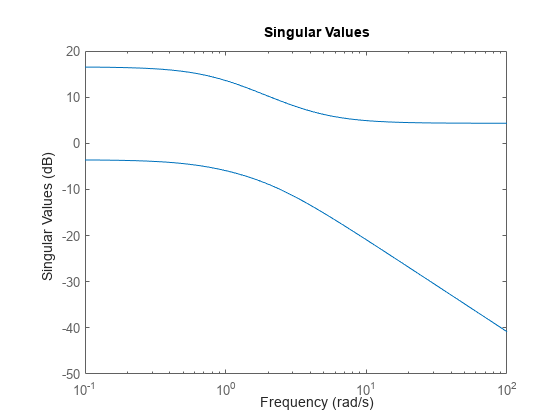
• Para representar valores singulares para varios sistemas dinámicos en la misma gráfica, puede especificar sys como lista de modelos separada por comas. Por ejemplo, sigma(sys1,sys2,sys3) representa los valores singulares para tres modelos en la misma gráfica.

• Para especificar un color, un estilo de línea y un marcador para cada sistema de la gráfica, especifique un valor LineSpec para cada sistema. Por ejemplo, sigma(sys1,LineSpec1,sys2,LineSpec2) representa dos modelos y especifica su estilo de gráfica. Para obtener más información sobre cómo especificar un valor LineSpec, consulte sigmaplot.

Ejemplos

Gráfica de valores singulares de un sistema dinámico

Cree una gráfica de valores singulares del siguiente sistema dinámico SISO en tiempo continuo.

$$\mathit{H}\left(\mathit{s}\right)=\frac{{\mathit{s}}^2+0.1\mathit{s}+7.5}{{\mathit{s}}^4+0.12{\mathit{s}}^3+9{\mathit{s}}^2}$$

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
sigma(H)

sigma selecciona automáticamente el rango del diagrama en función de la dinámica del sistema.

Gráfica sigma en frecuencias especificadas

Cree una gráfica de valores singulares sobre un rango de frecuencia especificado. Utilice este enfoque cuando desee centrarse en la dinámica de un rango de frecuencia en particular.

H = tf([-0.1,-2.4,-181,-1950],[1,3.3,990,2600]);
sigma(H,{1,100})
grid on

El arreglo de celdas {1,100} especifica el valor de frecuencia mínimo y máximo de la gráfica. Cuando establece límites de frecuencia de esta manera, la función selecciona los puntos intermedios para los datos de respuesta en frecuencia.

Como alternativa, especifique un vector de puntos de frecuencia para utilizar cuando evalúe y represente la respuesta en frecuencia.

w = [1 5 10 15 20 23 31 40 44 50 85 100];
sigma(H,w,'.-')
grid on

sigma representa la respuesta en frecuencia solo en las frecuencias especificadas.

Comparar gráficas de valores singulares de varios sistemas dinámicos

Compare la respuesta en frecuencia de un sistema en tiempo continuo con un sistema discretizado equivalente en la misma gráfica de valores singulares.

Cree sistemas dinámicos en tiempo continuo y tiempo discreto.

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
Hd = c2d(H,0.5,'zoh');

Cree una gráfica que muestre ambos sistemas.

sigma(H,Hd)
legend("Continuous","Discrete")

La gráfica sigma de un sistema en tiempo discreto incluye una línea vertical que marca la frecuencia Nyquist del sistema.

Gráfica de valores singulares con atributos de línea especificados

Especifique el estilo de línea, el color o el marcador en cada sistema de una gráfica sigma utilizando el argumento de entrada LineSpec.

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
Hd = c2d(H,0.5,'zoh');
sigma(H,'r',Hd,'b--')

La primera LineSpec, 'r', especifica una línea continua roja para la respuesta de H. La segunda LineSpec, 'b--', especifica una línea discontinua azul para la respuesta de Hd.

Obtener datos de valores singulares

Calcule los valores singulares de la respuesta en frecuencia de un sistema SISO.

Si no especifica frecuencias, sigma elige frecuencias en función de la dinámica del sistema y las devuelve en el segundo argumento de salida.

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
[sv,wout] = sigma(H);

Dado que H es un modelo SISO, la primera dimensión de sv es 1. La segunda dimensión es el número de frecuencias de wout.

size(sv)

ans = 1×2

     1    40

length(wout)

ans = 
40

De este modo, cada entrada a lo largo de la segunda dimensión de sv proporciona los valores singulares de la respuesta en la correspondiente frecuencia de wout.

Valores singulares de un sistema MIMO

Para este ejemplo, cree un sistema de dos salidas y tres entradas.

rng(0,'twister'); % For reproducibility
H = rss(4,2,3);

En este sistema, sigma representa los valores singulares de la matriz de la respuesta en frecuencia en la misma gráfica.

sigma(H)

Calcule los valores singulares en 20 frecuencias entre 1 y 10 radianes.

w = logspace(0,1,20);
sv = sigma(H,w);

sv es una matriz, en la que las filas se corresponden con los valores singulares de la matriz de respuesta en frecuencia y las columnas son valores de frecuencia. Examine las dimensiones.

size(sv)

ans = 1×2

     2    20

De este modo, por ejemplo, sv(:,10) son los valores singulares de la respuesta calculados en la 10.ª frecuencia de w.

Calcular y representar valores singulares

Considere el siguiente sistema dinámico de dos entradas y dos salidas.

$$H(s)=\left[\begin{array}{cc}0& {\displaystyle \frac{3s}{s^2+s+10}}\\ {\displaystyle \frac{s+1}{s+5}}& {\displaystyle \frac{2}{s+6}}\end{array}\right].$$

Calcule las respuestas de valores singulares de H(s) e I + H(s).

H = [0, tf([3 0],[1 1 10]) ; tf([1 1],[1 5]), tf(2,[1 6])];
[svH,wH] = sigma(H);
[svIH,wIH] = sigma(H,[],2);

En el último comando, la entrada 2 selecciona el segundo tipo de respuesta: I + H(s). Los vectores svH y svIH contienen los datos de respuesta de los valores singulares en las frecuencias en wH y wIH.

Represente las respuestas de los valores singulares de ambos sistemas.

subplot(211)
sigma(H)
subplot(212)
sigma(H,[],2)

Gráfica de valores singulares de un modelo con coeficientes complejos

Cree una gráfica de valores singulares de un modelo con coeficientes complejos y un modelo con coeficientes reales en la misma gráfica.

rng(0)
A = [-3.50,-1.25-0.25i;2,0];
B = [1;0];
C = [-0.75-0.5i,0.625-0.125i];
D = 0.5;
Gc = ss(A,B,C,D);
Gr = rss(4);
sigma(Gc,Gr)
legend('Complex-coefficient model','Real-coefficient model');

En la escala de frecuencia logarítmica, la gráfica muestra dos ramas para modelos con coeficientes complejos, una para las frecuencias positivas, con una flecha que apunta hacia la derecha, y otra para las frecuencias negativas, con una flecha que apunta hacia la izquierda. En ambas ramas, las flechas indican la dirección de las frecuencias que aumentan. Las gráficas para modelos con coeficientes reales siempre contienen una única rama sin flechas.

Puede modificar la escala de frecuencia de la gráfica haciendo clic con el botón secundario en la gráfica y seleccionando Properties. En el diálogo del editor de propiedades, en la pestaña Units, establezca la escala de frecuencia en linear scale. Como alternativa, puede utilizar la función sigmaplot y modificar las propiedades del objeto de gráfico.

Cree el diagrama con opciones personalizadas.

sp = sigmaplot(Gc,Gr);
sp.FrequencyScale = 'linear'

sp = 
  SigmaPlot (Singular Values) with properties:

          Responses: [2×1 controllib.chart.response.SigmaResponse]
    Characteristics: [1×1 controllib.chart.options.CharacteristicsManager]

      FrequencyUnit: "rad/s"
     FrequencyScale: "linear"
      MagnitudeUnit: "dB"
     MagnitudeScale: "linear"

            Visible: on

  Show all properties

legend('Complex-coefficient model','Real-coefficient model');

En la escala de frecuencia lineal, el diagrama muestra una única rama con un rango de frecuencia simétrico centrado en un valor de frecuencia de cero. La gráfica también muestra la respuesta en frecuencia negativa de un modelo con coeficientes reales cuando representa la respuesta junto con un modelo con coeficientes complejos.

Argumentos de entrada

sys — Sistema dinámico

modelo de sistema dinámico | arreglo de modelos

Sistema dinámico, especificado como un modelo de sistema dinámico SISO o MIMO, o bien un arreglo de modelos de sistemas dinámicos. Puede utilizar los siguientes tipos de sistemas dinámicos:

• Modelos LTI numéricos en tiempo continuo o en tiempo discreto, como modelos tf, zpk o ss.

• Modelos dispersos en espacio de estados, como modelos sparss o mechss. La cuadrícula de frecuencia w debe estar especificada para modelos dispersos.

• Modelos LTI generalizados o con incertidumbre, como modelos genss o uss (Robust Control Toolbox). El uso de modelos con incertidumbre requiere Robust Control Toolbox™.

  • En el caso de bloques de diseño de control ajustables, la función evalúa el modelo con su valor actual para representar la respuesta.

  • En el caso de los bloques de diseño de control con incertidumbre, la función representa el valor nominal y muestras aleatorias del modelo.

• Modelos de datos de respuesta en frecuencia, como modelos frd. Para estos modelos, la función representa la respuesta en las frecuencias definidas en el modelo.

• Modelos LTI identificados, como modelos idtf (System Identification Toolbox), idss (System Identification Toolbox) o idproc (System Identification Toolbox). El uso de modelos identificados requiere System Identification Toolbox™.

Si sys es un arreglo de modelos, la gráfica muestra las respuestas de todos los modelos del arreglo en los mismos ejes.

w — Frecuencias

{wmin,wmax} | vector | []

Frecuencias en las que se calcula la respuesta, especificadas como uno de los siguientes valores:

• Arreglo de celdas en formato {wmin,wmax}: calcula la respuesta en frecuencias entre wmin y wmax. Si wmax es superior a la frecuencia Nyquist de sys, la respuesta se calcula solo hasta la frecuencia Nyquist.

• Vector de frecuencias: calcula la respuesta en cada frecuencia especificada. Por ejemplo, utilice logspace para generar un vector fila con valores de frecuencia espaciados logarítmicamente. El vector w puede contener frecuencias positivas y negativas.

• []: selecciona automáticamente las frecuencias en función de la dinámica del sistema.

En el caso de modelos con coeficientes complejos, si especifica un rango de frecuencia de [w_min,w_max] para su diagrama, entonces en:

• La escala de frecuencia logarítmica, los límites de frecuencia del diagrama están establecidos en [w_min,w_max] y el diagrama muestra dos ramas, una para frecuencias positivas [w_min,w_max] y una para frecuencias negativas [–w_max,–w_min].

• La escala de frecuencia lineal, los límites de frecuencia del diagrama están establecidos en [–w_max,w_max] y el diagrama muestra una única rama con un rango de frecuencia simétrico centrado en un valor de frecuencia de cero.

Especifique frecuencias en unidades de rad/TimeUnit, donde TimeUnit es la propiedad TimeUnit del modelo.

type — Tipo de valores singulares modificados

1 | 2 | 3

Tipo de valores singulares modificados, especificados como una de las siguientes opciones:

• 1: representa los valores singulares de la respuesta en frecuencia H^–1, donde H es la respuesta en frecuencia de sys.

• 2: representa los valores singulares de la respuesta en frecuencia I+H.

• 3: representa los valores singulares de la respuesta en frecuencia I+H^-1.

Dependencias

Puede especificar type solo cuando sys tenga el mismo número de entradas y salidas.

Argumentos de salida

sv — Respuesta en frecuencia de valores singulares

matriz

Valores singulares de la respuesta en frecuencia en unidades absolutas, devueltas como una matriz. sv contiene los valores singulares calculados en las frecuencias w si las ha proporcionado, o wout si no lo hizo. En un sistema sys con Nu entradas y Ny salidas, sv cuenta con min(Nu,Ny) filas y tantas columnas como valores en w o wout. El valor sv(:,k) proporciona los valores singulares en un orden descendente en la frecuencia wout(k).

wout — Frecuencias

vector

Frecuencias en las que la función devuelve la respuesta del sistema, devueltas como un vector columna. La función elige los valores de frecuencia en función de la dinámica del modelo, a menos que especifique frecuencias con el argumento de entrada w.

wout también contiene valores de frecuencia negativos para modelos con coeficientes complejos.

Los valores de frecuencia se expresan en radianes por TimeUnit, donde TimeUnit es el valor de la propiedad TimeUnit de sys.

Sugerencias

• Cuando necesite opciones de personalización de gráficas adicionales, utilice en su lugar sigmaplot.

• Las gráficas creadas con sigma no admiten títulos ni etiquetas multilínea especificados como arreglos de cadenas o arreglos de celdas de vectores de caracteres. Para especificar títulos y etiquetas multilínea, utilice una cadena única con un carácter newline.

  sigma(sys)
  title("first line" + newline + "second line");

Algoritmos

sigma utiliza la función MATLAB^® de svd para calcular los valores singulares de la respuesta en frecuencia compleja.

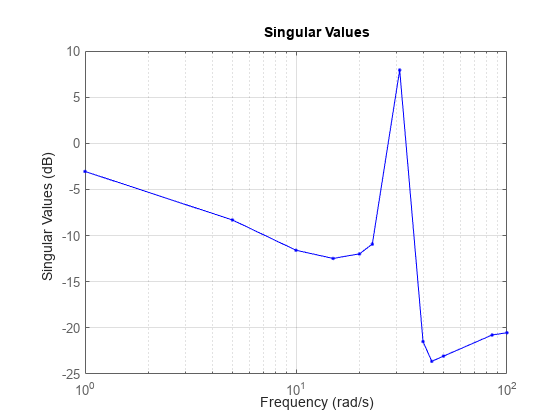
• En un modelo frd, sigma calcula los valores singulares de sys.ResponseData en las frecuencias sys.Frequency.

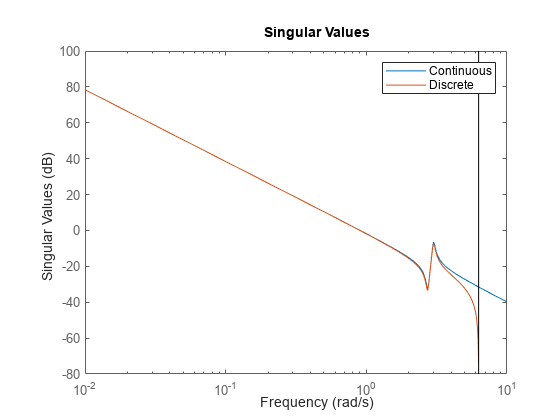
• En el caso de modelos en tiempo continuo tf, ss o zpk con función de transferencia H(s), sigma calcula los valores singulares de H(jω) como una función de la frecuencia ω.

• En los modelos en tiempo discreto tf, ss o zpk con función de transferencia H(z) y tiempo de muestreo T_s, sigma calcula los valores singulares de

  $$H\left(e^{j\omega T_s}\right)$$

  para frecuencias ω entre 0 y la frecuencia Nyquist ω_N = n/T_s.

Historial de versiones

Introducido antes de R2006a

R2024b: gca ahora devuelve un objeto de gráfico

En el caso de gráficas creadas con sigma, la función gca ahora devuelve un objeto de gráfico sigmaplot en lugar de un eje dentro de la gráfica.

Consulte también

sigmaplot | freqresp | nyquist | bode

Temas

• Respuestas en el dominio de la frecuencia
• Modelos de sistemas dinámicos