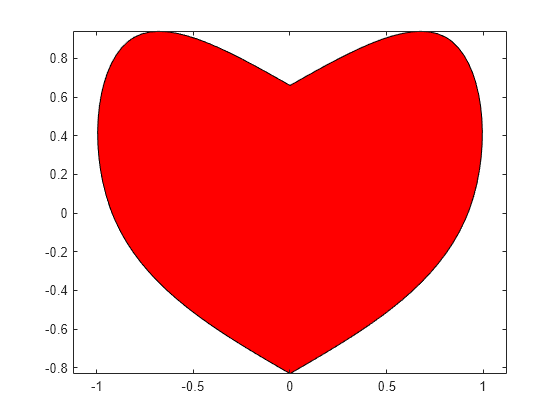cscvn

Curva de spline cúbico interpolante "natural" o periódica

Sintaxis

curve = cscvn(points)

Descripción

curve = cscvn(points) devuelve una curva de spline cúbico paramétrica variacional o natural, (en formato ppform) que pasa por los puntos de la secuencia proporcionados (:j), j = 1:end. El valor del parámetro t(j) para el j-ésimo punto sigue el esquema centrípeto de Eugene Lee [1], como raíz cuadrada acumulada de longitud de cuerda:

$${\displaystyle \sum _{i<j}\sqrt{\Vert \text{points}(:,i+1)-\text{points }(:,i)\Vert {}_2}}$$

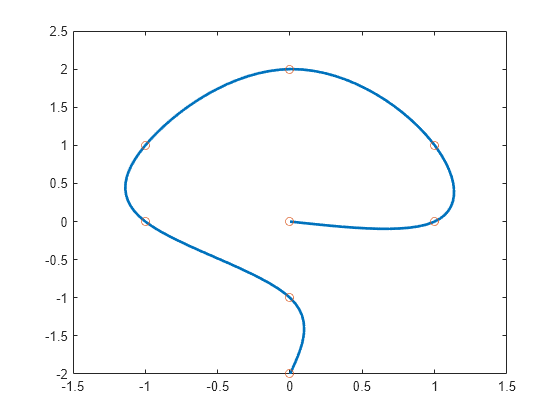
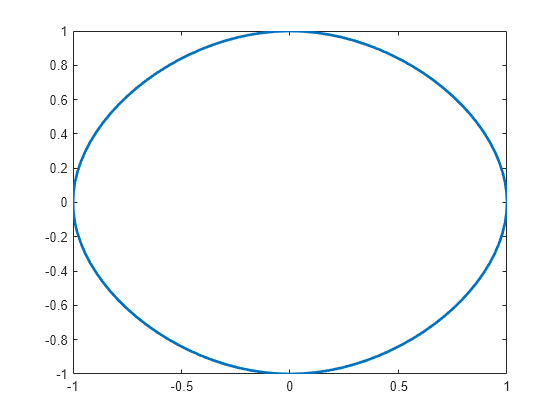
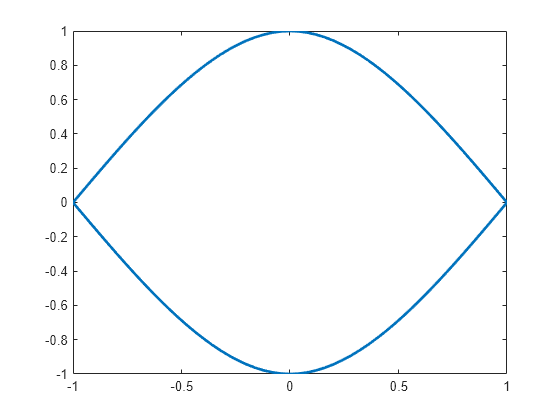
Si el primer y el último punto coinciden y no hay otros puntos repetidos, la función construye una curva de spline cúbico periódica. Sin embargo, los puntos dobles resultan en esquinas.

Ejemplos

Representar curvas de spline cúbico interpolantes

Este ejemplo muestra cómo construir y representar varias curvas de spline cúbico interpolantes utilizando la función cscvn.

Este código genera una secuencia de puntos y, a continuación, representa el spline cúbico generado con la función cscvn. Los puntos elegidos se marcan como círculos:

points=[0 1 1 0 -1 -1 0 0; 0 0 1 2 1 0 -1 -2]; 
fnplt(cscvn(points)); hold on, 
plot(points(1,:),points(2,:),'o'), hold off

Este código representa una curva circular que atraviesa los cuatro vértices del rombo estándar (debido a las condiciones de límite periódicas impuestas):

 fnplt(cscvn( [1 0 -1    0 1;0 1 0   -1 0] ))

Este código muestra una esquina en el punto doble, así como en el extremo de la curva:

 fnplt(cscvn( [1 0 -1 -1 0 1;0 1 0 0 -1 0] ))

Por último, este código genera una curva cerrada con un punto doble, que resulta en una esquina. Dedíqueselo a sus seres queridos.

c=fnplt(cscvn([0 .82 .92 0 0 -.92 -.82 0; .66 .9 0 ...
-.83 -.83 0 .9 .66])); fill(c(1,:),c(2,:),'r'), axis equal

Argumentos de entrada

points — Secuencia de puntos

escalar | vector | matriz

Secuencia de puntos en los que se interpola el spline cúbico "natural" paramétrico, especificada como escalar, vector o matriz.

Argumentos de salida

curve — Spline en formato ppform

estructura de spline

Spline en formato ppform, devuelto como estructura con los siguientes campos.

Form — Forma del spline

pp

Forma del spline, devuelta como pp. pp indica que el spline tiene forma polinomial por tramos.

Breaks — Ubicaciones de los nudos del spline

vector | arreglo de celdas

Posiciones de los nudos del spline, devueltas como un vector o un arreglo de celdas de vectores en el caso de datos multivariantes. Los vectores contienen elementos estrictamente crecientes que representan el inicio y el fin de cada uno de los intervalos en los que se definen los tramos polinomiales.

Coefs — Coeficientes de los polinomios

matriz | arreglo

Coeficientes de los polinomios para cada tramo, devueltos como una matriz o como un arreglo en el caso de datos multivariantes.

Pieces — Número de tramos polinomiales

escalar | vector

Número de tramos polinomiales que describen el spline, devuelto como un escalar o como un vector de números de tramos de cada variable en el caso de datos multivariantes.

Order — Orden de los polinomios

escalar | vector

Orden de la función polinómica que describe cada tramo polinomial del spline, devuelta como un escalar o como un vector que contiene el orden de cada variable en el caso de datos multivariantes.

Dim — Dimensionalidad

escalar

Dimensionalidad de la función de destino, devuelta como un escalar.

Algoritmos

cscvn determina la secuencia de salto t como

$$t_k=\{\begin{array}{l}0,k=1\\ {{\displaystyle \sum _{i=1}^{k-1}\left({\displaystyle \sum _{j=1}^d{(p_{i+1,j}-p_{i,j})}^2}\right)}}^{\frac{1}{4}},k>1\end{array}$$

donde t_k es el elemento en la posición k en t, 1 ≤ k ≤ n–1, y p es la traspuesta de la matriz points de d por n. Si points contiene puntos repetidos, cscvn utiliza csape con condiciones de contorno periódicas o variacionales para crear tramos suaves. cscvn devuelve la secuencia de salto t en el campo breaks del argumento de salida curve.

Referencias

[1] E. T. Y. Lee. “Choosing nodes in parametric curve interpolation.” Computer-Aided Design 21 (1989), 363–370.

Historial de versiones

Introducido en R2006b

Consulte también

csape | fnplt | getcurve

Temas

• Introducción al ajuste de splines
• El ppform