Definir capas de deep learning personalizadas
Sugerencia
En esta sección se explica cómo definir capas de deep learning personalizadas para usarlas en sus problemas. Para ver una lista de capas integradas en Deep Learning Toolbox™, consulte Lista de capas de deep learning.
Si Deep Learning Toolbox no proporciona la capa que necesita para la tarea, puede definir su propia capa personalizada usando este tema como guía. Después de definir la capa personalizada, puede comprobar automáticamente que es válida y compatible con la GPU, y que devuelve como salida gradientes correctamente definidos.
Arquitectura de capas de red neuronal
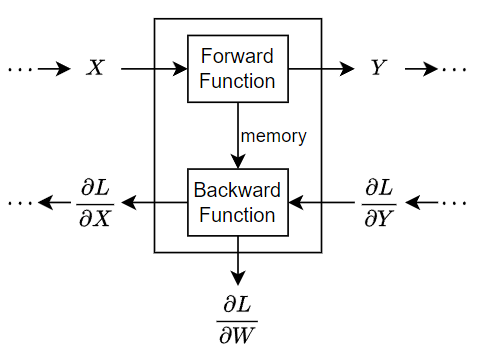
Durante el entrenamiento, el software realiza de forma iterativa pases hacia delante y hacia atrás a través de la red.
Durante un pase hacia delante a través de la red, cada capa coge las salidas de las capas anteriores, aplica una función y luego devuelve como salida (propagación hacia delante) los resultados a las siguientes capas. Las capas que tienen estado, como las capas de LSTM, también actualizan su estado.
Las capas pueden tener varias entradas o salidas. Por ejemplo, una capa puede coger X1, …, XN de varias capas anteriores y propagar hacia delante las salidas Y1, …, YM a las siguientes capas.
Al final de cada pase hacia delante de la red, el software calcula la pérdida L entre las predicciones y los objetivos.
Durante el pase hacia atrás a través de la red, cada capa coge las derivadas de la pérdida con respecto a las salidas de la capa, calcula las derivadas de la pérdida L con respecto a las entradas y propaga los resultados hacia atrás. Si la capa cuenta con parámetros que se aprenden, también calculará las derivadas de los pesos de la capa (parámetros que se aprenden). El software usa las derivadas de los pesos para actualizar los parámetros que se aprenden. Para ahorrar cálculos, la siguiente función puede compartir información con la función de retropropagación usando una salida de memoria opcional.
Este gráfico muestra el flujo de datos a través de una red neuronal profunda y destaca el flujo de datos a través de una capa con una única entrada X, una única salida Y y un parámetro que se aprende W.
Plantilla de capa personalizada
Para definir una capa personalizada, use esta plantilla de definición de clase. Esta plantilla proporciona la estructura de una definición de clase de capa personalizada. Esboza lo siguiente:
Los bloques opcionales
propertiespara las propiedades de la capa, los parámetros que se aprenden y los parámetros de estado. Para obtener más información, consulte Propiedades de capas personalizadas.La función de constructor de la capa.
La función
predicty la función opcionalforward. Para obtener más información, consulte Funciones hacia delante.La función opcional
resetStatepara capas con propiedades de estado. Para obtener más información, consulte Función de restablecimiento del estado.La función opcional
backward. Para obtener más información, consulte Función de retropropagación.
classdef myLayer < nnet.layer.Layer % ... % & nnet.layer.Formattable ... % (Optional) % & nnet.layer.Acceleratable % (Optional) properties % (Optional) Layer properties. % Declare layer properties here. end properties (Learnable) % (Optional) Layer learnable parameters. % Declare learnable parameters here. end properties (State) % (Optional) Layer state parameters. % Declare state parameters here. end properties (Learnable, State) % (Optional) Nested dlnetwork objects with both learnable % parameters and state parameters. % Declare nested networks with learnable and state parameters here. end methods function layer = myLayer() % (Optional) Create a myLayer. % This function must have the same name as the class. % Define layer constructor function here. end function layer = initialize(layer,layout) % (Optional) Initialize layer learnable and state parameters. % % Inputs: % layer - Layer to initialize % layout - Data layout, specified as a networkDataLayout % object % % Outputs: % layer - Initialized layer % % - For layers with multiple inputs, replace layout with % layout1,...,layoutN, where N is the number of inputs. % Define layer initialization function here. end function [Y,state] = predict(layer,X) % Forward input data through the layer at prediction time and % output the result and updated state. % % Inputs: % layer - Layer to forward propagate through % X - Input data % Outputs: % Y - Output of layer forward function % state - (Optional) Updated layer state % % - For layers with multiple inputs, replace X with X1,...,XN, % where N is the number of inputs. % - For layers with multiple outputs, replace Y with % Y1,...,YM, where M is the number of outputs. % - For layers with multiple state parameters, replace state % with state1,...,stateK, where K is the number of state % parameters. % Define layer predict function here. end function [Y,state,memory] = forward(layer,X) % (Optional) Forward input data through the layer at training % time and output the result, the updated state, and a memory % value. % % Inputs: % layer - Layer to forward propagate through % X - Layer input data % Outputs: % Y - Output of layer forward function % state - (Optional) Updated layer state % memory - (Optional) Memory value for custom backward % function % % - For layers with multiple inputs, replace X with X1,...,XN, % where N is the number of inputs. % - For layers with multiple outputs, replace Y with % Y1,...,YM, where M is the number of outputs. % - For layers with multiple state parameters, replace state % with state1,...,stateK, where K is the number of state % parameters. % Define layer forward function here. end function layer = resetState(layer) % (Optional) Reset layer state. % Define reset state function here. end function [dLdX,dLdW,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory) % (Optional) Backward propagate the derivative of the loss % function through the layer. % % Inputs: % layer - Layer to backward propagate through % X - Layer input data % Y - Layer output data % dLdY - Derivative of loss with respect to layer % output % dLdSout - (Optional) Derivative of loss with respect % to state output % memory - Memory value from forward function % Outputs: % dLdX - Derivative of loss with respect to layer input % dLdW - (Optional) Derivative of loss with respect to % learnable parameter % dLdSin - (Optional) Derivative of loss with respect to % state input % % - For layers with state parameters, the backward syntax must % include both dLdSout and dLdSin, or neither. % - For layers with multiple inputs, replace X and dLdX with % X1,...,XN and dLdX1,...,dLdXN, respectively, where N is % the number of inputs. % - For layers with multiple outputs, replace Y and dLdY with % Y1,...,YM and dLdY,...,dLdYM, respectively, where M is the % number of outputs. % - For layers with multiple learnable parameters, replace % dLdW with dLdW1,...,dLdWP, where P is the number of % learnable parameters. % - For layers with multiple state parameters, replace dLdSin % and dLdSout with dLdSin1,...,dLdSinK and % dLdSout1,...,dldSoutK, respectively, where K is the number % of state parameters. % Define layer backward function here. end end end
Entradas y salidas con formato
Usar objetos dlarray facilita el trabajo con datos de múltiples dimensiones, ya que permite etiquetar las dimensiones. Por ejemplo, puede etiquetar qué dimensiones corresponden a las dimensiones de espacio, tiempo, canal y lote usando las etiquetas "S", "T", "C" y "B", respectivamente. Para dimensiones no especificadas y otras dimensiones, use la etiqueta "U". Para las funciones de objeto dlarray que operan sobre dimensiones concretas, puede especificar las etiquetas de dimensión formateando el objeto dlarray directamente o usando la opción DataFormat.
Usar objetos dlarray con formato en funciones de capas también permite definir capas en las que las entradas y salidas tienen formatos diferentes, como las capas que permutan, añaden o eliminan dimensiones. Por ejemplo, puede definir una capa que tome como entrada un minilote de imágenes con el formato "SSCB" (espacial, espacial, canal, lote) y como salida un minilote de secuencias con el formato "CBT" (canal, lote, tiempo). Usar objetos dlarray con formato también permite definir capas que pueden operar sobre datos con diferentes formatos de entrada, como capas que admiten entradas con los formatos "SSCB" (espacial, espacial, canal, lote) y "CBT" (canal, lote, tiempo).
Puede especificar cómo procesar datos con y sin formato que el software pasa a y desde la capa optando por heredarlos de la clase nnet.layer.Formattable. Esta tabla describe cómo procesa el software datos con y sin formato en capas personalizadas.
| Definición de la capa | Procesamiento de datos de entrada | Procesamiento de datos de salida |
|---|---|---|
Hereda de nnet.layer.Formattable | El software pasa la entrada de la capa a la función de capas directamente:
| El software pasa las salidas de la función de capas a las capas posteriores directamente:
Advertencia Para capas personalizadas que heredan de
|
No hereda de nnet.layer.Formattable | El software elimina los formatos de cualquier entrada con formato y pasa los datos sin formato a la función de capas:
| Los datos de salida no deben tener formato. El software aplica los formatos de las entradas de la capa a cualquier salida de la función de capas que no tenga formato y pasa el resultado a las capas posteriores:
|
Para ver un ejemplo de cómo definir una capa personalizada con entradas con formato, consulte Define Custom Deep Learning Layer with Formatted Inputs.
Aceleración de capas personalizadas
Si no se especifica una función de retropropagación al definir una capa personalizada, el software determina automáticamente los gradientes usando la diferenciación automática.
Cuando se entrena una red con una capa personalizada sin función de retropropagación, el software traza cada objeto dlarray de entrada de la función hacia adelante de la capa personalizada para determinar la gráfica de cálculo que se usa para la diferenciación automática. Este proceso de trazado puede llevar algo de tiempo y terminar recalculando el mismo trazado. Mediante la optimización, el almacenamiento en caché y la reutilización de los trazados, se puede acelerar el cálculo del gradiente al entrenar una red. El software también puede reutilizar estos trazados para acelerar las predicciones de la red después del entrenamiento.
El trazado depende del tamaño, el formato y el tipo de datos subyacentes de las entradas de la capa. Es decir, la capa activa un nuevo trazado para las entradas con un tamaño, formato o tipo de datos subyacente no contenidos en la memoria caché. Las entradas que solo se diferencien en el valor de un trazado previamente almacenado en caché no activan otro nuevo.
Para indicar que la capa personalizada admite aceleración, herede también de la clase nnet.layer.Acceleratable al definir la capa personalizada. Cuando una capa personalizada hereda de nnet.layer.Acceleratable, el software almacena automáticamente en caché los trazados al pasar datos a través de un objeto dlnetwork.
Por ejemplo, para indicar que la capa personalizada myLayer admite aceleración, use esta sintaxis
classdef myLayer < nnet.layer.Layer & nnet.layer.Acceleratable ... end
Consideraciones relativas a la aceleración
Debido a la naturaleza de los trazados en caché, no todas las funciones admiten la aceleración.
El proceso de almacenamiento en caché puede guardar valores o estructuras de código que cabría esperar que cambiaran o que dependieran de factores externos. Debe tener cuidado al acelerar capas personalizadas que:
Generen números aleatorios.
Usen instrucciones
ify bucleswhilecon condiciones que dependan de los valores de los objetosdlarray.
Dado que el proceso de almacenamiento en caché requiere un cálculo adicional, la aceleración puede hacer que, en algunos casos, el código tarde más en ejecutarse. Este escenario puede darse cuando el software dedica tiempo a crear nuevas memorias caché que no se reutilizan con frecuencia. Por ejemplo, cuando se pasan varios minilotes de diferentes longitudes de secuencia a la función, el software activa un nuevo trazado para cada longitud de secuencia única.
Cuando la aceleración de capas personalizadas causa ralentización, puede desactivar la aceleración eliminando la clase Acceleratable o desactivando la aceleración de las funciones predict y forward del objeto dlnetwork estableciendo la opción Acceleration en "none".
Para obtener más información sobre cómo activar el soporte para la aceleración de capas personalizadas, consulte Custom Layer Function Acceleration.
Propiedades de capas personalizadas
Declare las propiedades de la capa en la sección properties de la definición de la clase.
De forma predeterminada, las capas personalizadas tienen estas propiedades. No declare estas propiedades en la sección properties.
| Propiedad | Descripción |
|---|---|
Name | Nombre de la capa, especificado como un vector de caracteres o un escalar de cadena. Para entradas en forma de arreglo Layer, las funciones trainnet y dlnetwork asignan automáticamente nombres a las capas sin nombre. |
Description | Descripción de una línea de la capa, especificada como un escalar de cadena o un vector de caracteres. Esta descripción aparece cuando se muestra un arreglo de objetos Si no especifica una descripción de capa, el software muestra el nombre de la clase de capa. |
Type | Tipo de la capa, especificado como un vector de caracteres o un escalar de cadena. El valor de Si no especifica un tipo de capa, el software muestra el nombre de la clase de capa. |
NumInputs | Número de entradas de la capa, especificado como entero positivo. Si no especifica este valor, el software establece automáticamente NumInputs en el número de nombres de InputNames. El valor predeterminado es 1. |
InputNames | Nombres de entrada de la capa, especificados como un arreglo de celdas de vectores de caracteres. Si no especifica este valor y NumInputs es mayor que 1, el software establece automáticamente InputNames en {'in1',...,'inN'}, donde N es igual a NumInputs. El valor predeterminado es {'in'}. |
NumOutputs | Número de salidas de la capa, especificado como entero positivo. Si no especifica este valor, el software establece automáticamente NumOutputs en el número de nombres de OutputNames. El valor predeterminado es 1. |
OutputNames | Nombres de salida de la capa, especificados como un arreglo de celdas de vectores de caracteres. Si no especifica este valor y NumOutputs es mayor que 1, el software establece automáticamente OutputNames en {'out1',...,'outM'}, donde M es igual a NumOutputs. El valor predeterminado es {'out'}. |
Si la capa no tiene otras propiedades, puede omitir la sección properties.
Sugerencia
Si está creando una capa con varias entradas, debe establecer las propiedades NumInputs o InputNames en el constructor de la capa. Si está creando una capa con varias salidas, debe establecer las propiedades NumOutputs o OutputNames en el constructor de la capa. Para ver un ejemplo, consulte Define Custom Deep Learning Layer with Multiple Inputs.
Parámetros que se pueden aprender
Declare los parámetros de la capa que se pueden aprender en la sección properties (Learnable) de la definición de la clase.
Puede especificar arreglos numéricos u objetos dlnetwork como parámetros que se pueden aprender. Si el objeto dlnetwork tiene parámetros que se pueden aprender y parámetros de estado (por ejemplo, un objeto dlnetwork que contiene una capa LSTM), debe especificarlo en la sección properties (Learnable, State). Si la capa no tiene parámetros que se pueden aprender, podrá omitir las secciones properties con el atributo Learnable.
Si lo desea, puede especificar el factor de la tasa de aprendizaje y el factor L2 de los parámetros que se pueden aprender. De forma predeterminada, cada parámetro que se puede aprender tiene un factor de tasa de aprendizaje y un factor L2 establecidos en 1. Tanto para las capas integradas como para las personalizadas, puede establecer y obtener los factores de la tasa de aprendizaje y los factores de regularización L2 mediante las siguientes funciones.
| Función | Descripción |
|---|---|
setLearnRateFactor | Establece el factor de la tasa de aprendizaje de un parámetro que se puede aprender. |
setL2Factor | Establece el factor de regularización L2 de un parámetro que se puede aprender. |
getLearnRateFactor | Obtiene el factor de la tasa de aprendizaje de un parámetro que se puede aprender. |
getL2Factor | Obtiene el factor de regularización L2 de un parámetro que se puede aprender. |
Para especificar el factor de la tasa de aprendizaje y el factor L2 de un parámetro que se puede aprender, use las sintaxis layer = setLearnRateFactor(layer,parameterName,value) y layer = setL2Factor(layer,parameterName,value), respectivamente.
Para obtener el valor del factor de la tasa de aprendizaje y del factor L2 de un parámetro que se puede aprender, use las sintaxis getLearnRateFactor(layer,parameterName) y getL2Factor(layer,parameterName), respectivamente.
Por ejemplo, esta sintaxis establece el factor de la tasa de aprendizaje del parámetro que se puede aprender "Alpha" en 0.1.
layer = setLearnRateFactor(layer,"Alpha",0.1);Parámetros de estado
En el caso de las capas con estado, como las capas recurrentes, declare los parámetros de estado de la capa en la sección properties (State) de la definición de la clase. Si el parámetro que se puede aprender es un objeto dlnetwork que tiene parámetros que se pueden aprender y parámetros de estado (por ejemplo, un objeto dlnetwork que contiene una capa LSTM), debe especificar la propiedad correspondiente en la sección properties (Learnable, State). Si la capa no tiene parámetros de estado, podrá omitir las secciones properties con el atributo State.
Si la capa tiene parámetros de estado, las funciones hacia delante deben devolver también el estado actualizado de la capa. Para obtener más información, consulte Funciones hacia delante.
Para especificar una función de estado de restablecimiento personalizada, incluya una función con la sintaxis layer = resetState(layer) en la definición de la clase. Para obtener más información, consulte Función de restablecimiento del estado.
No se admite el entrenamiento paralelo de redes que contengan capas personalizadas con parámetros de estado que usen la función trainnet. Cuando se entrena una red con capas personalizadas con parámetros de estado, la opción de entrenamiento ExecutionEnvironment debe ser "auto", "gpu" o "cpu".
Inicialización de parámetros que se pueden aprender y de estado
Puede indicar que se inicialicen los parámetros que se pueden aprender y los parámetros de estado de la capa en la función de construcción de la capa o en una función initialize personalizada:
Si la inicialización de los parámetros que se pueden aprender o de los parámetros de estado no requiere información sobre el tamaño de la entrada de la capa (por ejemplo, los pesos que se pueden aprender de una capa de suma ponderada son vectores cuyo tamaño coincide con el número de entradas de la capa), puede inicializar los pesos en la función de construcción de la capa. Para ver un ejemplo, consulte Define Custom Deep Learning Layer with Multiple Inputs.
Si la inicialización de los parámetros que se pueden aprender o de los parámetros de estado requiere información sobre el tamaño de la entrada de la capa (por ejemplo, los pesos que se pueden aprender de una capa SReLU son vectores cuyo tamaño coincide con el número de entradas de la capa), puede inicializar los pesos en la función de construcción de la capa. Para ver un ejemplo, consulte Define Custom Deep Learning Layer with Learnable Parameters.
Funciones hacia delante
Algunas capas se comportan de forma diferente durante el entrenamiento y durante la predicción. Por ejemplo, una capa de abandono realiza el abandono solo durante el entrenamiento y no tiene ningún efecto durante la predicción. Una capa usa una de estas dos funciones para realizar un pase hacia delante: predict o forward. Si el pase hacia adelante es en el momento de la predicción, la capa usa la función predict. Si el pase hacia adelante es en el momento del entrenamiento, la capa usa la función forward. Si no necesita dos funciones diferentes para el momento de la predicción y el momento del entrenamiento, puede omitir la función forward. En caso de necesitarlas, la capa usa predict en el momento del entrenamiento.
Si la capa tiene parámetros de estado, las funciones hacia delante deben devolver los parámetros de estado actualizados de la capa como arreglos numéricos.
Si define tanto una función forward personalizada como una función backward personalizada, la función hacia delante debe devolver una salida memory.
La sintaxis de la función predict depende del tipo de capa.
Y = predict(layer,X)reenvía los datos de entradaXa través de la capa y devuelve como salida el resultadoY, dondelayertiene una única entrada y una única salida.[Y,state] = predict(layer,X)también devuelve como salida el parámetro de estado actualizadostate, dondelayertiene un único parámetro de estado.
Puede ajustar las sintaxis para capas con varias entradas, varias salidas o varios parámetros de estado:
Para capas con varias entradas, sustituya
XporX1,...,XN, dondeNes el número de entradas. La propiedadNumInputsdebe coincidir conN.Para capas con varias salidas, sustituya
YporY1,...,YM, dondeMes el número de salidas. La propiedadNumOutputsdebe coincidir conM.Para capas con varios parámetros de estado, sustituya
stateporstate1,...,stateK, dondeKes el número de parámetros de estado.
Sugerencia
Si el número de entradas en la capa puede variar, use varargin en lugar de X1,…,XN. En este caso, varargin es un arreglo de celdas de las entradas, donde varargin{i} corresponde a Xi.
Si el número de salidas puede variar, use varargout en lugar de Y1,…,YM. En este caso, varargout es un arreglo de celdas de las salidas, donde varargout{j} corresponde a Yj.
Sugerencia
Si la capa personalizada tiene un objeto dlnetwork para un parámetro que se puede aprender, en la función predict de la capa personalizada, use la función predict para dlnetwork. Al hacerlo, la función predict del objeto dlnetwork usa las operaciones de capa adecuadas para realizar la predicción. Si el objeto dlnetwork tiene parámetros de estado, también devuelve el estado de la red.
La sintaxis de la función forward depende del tipo de capa:
Y = forward(layer,X)reenvía los datos de entradaXa través de la capa y devuelve como salida el resultadoY, dondelayertiene una única entrada y una única salida.[Y,state] = forward(layer,X)también devuelve como salida el parámetro de estado actualizadostate, dondelayertiene un único parámetro de estado.[__,memory] = forward(layer,X)también devuelve un valor de memoria para una funciónbackwardpersonalizada mediante cualquiera de las sintaxis anteriores. Si la capa tiene tanto una funciónforwardpersonalizada como una funciónbackwardpersonalizada, la función hacia delante debe devolver un valor de memoria.
Puede ajustar las sintaxis para capas con varias entradas, varias salidas o varios parámetros de estado:
Para capas con varias entradas, sustituya
XporX1,...,XN, dondeNes el número de entradas. La propiedadNumInputsdebe coincidir conN.Para capas con varias salidas, sustituya
YporY1,...,YM, dondeMes el número de salidas. La propiedadNumOutputsdebe coincidir conM.Para capas con varios parámetros de estado, sustituya
stateporstate1,...,stateK, dondeKes el número de parámetros de estado.
Sugerencia
Si el número de entradas en la capa puede variar, use varargin en lugar de X1,…,XN. En este caso, varargin es un arreglo de celdas de las entradas, donde varargin{i} corresponde a Xi.
Si el número de salidas puede variar, use varargout en lugar de Y1,…,YM. En este caso, varargout es un arreglo de celdas de las salidas, donde varargout{j} corresponde a Yj.
Sugerencia
Si la capa personalizada tiene un objeto dlnetwork para un parámetro que se puede aprender, en la función forward de la capa personalizada, use la función forward del objeto dlnetwork. Al hacerlo, la función forward del objeto dlnetwork usa las operaciones de capa adecuadas para realizar el entrenamiento.
Las dimensiones de las entradas dependen del tipo de datos y de la salida de las capas conectadas.
| Entrada de la capa | Ejemplo | |
|---|---|---|
| Forma | Formato de los datos | |
| Imágenes 2D | Arreglo numérico de h por w por c por N, donde h, w, c y N son la altura, la anchura, el número de canales de las imágenes y el número de observaciones, respectivamente. | "SSCB" |
| Imágenes 3D | Arreglo numérico de h por w por d por c por N, en el que h, w, d, c y N son la altura, la anchura, el número de canales de las imágenes y el número de observaciones de las imágenes, respectivamente. | "SSSCB" |
| Secuencias de vectores | Matriz de c por N por s, donde c es el número de características de la secuencia, N es el número de observaciones de la secuencia y s es la longitud de la secuencia. | "CBT" |
| Secuencias de imágenes 2D | Arreglo de h por w por c por N por s, donde h, w y c corresponden a la altura, la anchura y el número de canales de la imagen, respectivamente, N es el número de observaciones de la secuencia de la imagen y s es la longitud de la secuencia. | "SSCBT" |
| Secuencias de imágenes 3D | Arreglo de h por w por d por c por N por s, donde h, w, d y c corresponden a la altura, la anchura, la profundidad y el número de canales de la imagen, respectivamente, N es el número de observaciones de la secuencia de la imagen y s es la longitud de la secuencia. | "SSSCBT" |
| Características | Arreglo de c por N, donde c es el número de características y N es el número de observaciones. | "CB" |
Las capas que producen secuencias como salida pueden producir secuencias de cualquier longitud o datos sin dimensión de tiempo.
Las salidas de la función hacia delante de la capa personalizada pueden ser de valor complejo. (desde R2024a) Si la capa genera como salida datos de valor complejo, cuando use la capa personalizada en una red neuronal, debe asegurarse de que las capas posteriores o la función de pérdida sean compatibles con entradas de valor complejo. Usar números complejos en las funciones predict o forward de su capa personalizada puede dar lugar a parámetros complejos que se pueden aprender. Para entrenar modelos con parámetros que se pueden aprender de valor complejo, utilice la función trainnet con los solvers "sgdm" "adam" o "rmsprop", especificándolos con la función trainingOptions, o utilice un bucle de entrenamiento personalizado con las funciones sgdmupdate, adamupdate o rmspropupdate.
Antes de R2024a: Las salidas de las funciones hacia delante de la capa personalizada no deben ser complejas. Si las funciones predict o forward de su capa personalizada implican números complejos, convierta todas las salidas a valores reales antes de devolverlas. Usar números complejos en las funciones predict o forward de su capa personalizada puede dar lugar a parámetros complejos que se pueden aprender. Si usa la diferenciación automática (es decir, no está escribiendo una función de retropropagación para la capa personalizada), convierta todos los parámetros que se pueden aprender en valores reales al principio del cálculo de la función. De este modo, se garantiza que el algoritmo de diferenciación automática no genere como salida gradientes de valor complejo.
Función de restablecimiento del estado
De forma predeterminada, la función resetState para objetos dlnetwork no tiene ningún efecto sobre las capas personalizadas con parámetros de estado. Para definir el comportamiento de capa de la función resetState para objetos de red, defina la función de capa resetState opcional en la definición de capa que restablece los parámetros de estado.
La función resetState debe tener la sintaxis layer = resetState(layer), donde la capa devuelta tiene las propiedades de restablecimiento de estado.
La función resetState no debe establecer ninguna propiedad de capa, excepto aquellas que se pueden aprender y las propiedades de estado. Si la función establece otras propiedades de la capa, esta podría comportarse de forma inesperada. (desde R2023a)
Función de retropropagación
La función de retropropagación de la capa calcula las derivadas de la pérdida con respecto a los datos de entrada y, a continuación, devuelve como salida (propaga hacia atrás) los resultados a la capa anterior. Si la capa tiene parámetros que se pueden aprender (por ejemplo, los pesos de la capa), backward también calcula las derivadas de estos. Cuando se usa la función trainnet, la capa actualiza automáticamente los parámetros que se pueden aprender usando estas derivadas durante el paso hacia atrás.
Definir la función de retropropagación es opcional. Si no se especifica una función de retropropagación y las funciones hacia delante de la capa admiten objetos dlarray, el software determina automáticamente la función de retropropagación mediante diferenciación automática. Para obtener una lista de las funciones que admiten objetos dlarray, consulte List of Functions with dlarray Support. Defina una función de retropropagación personalizada cuando desee:
Usar un algoritmo específico para calcular las derivadas.
Usar operaciones en las funciones hacia delante que no admitan objetos
dlarray.
Las capas personalizadas con objetos dlnetwork que se pueden aprender no admiten funciones de retropropagación personalizadas.
Para definir una función de retropropagación personalizada, cree una denominada backward.
La sintaxis de la función backward depende del tipo de capa.
dLdX = backward(layer,X,Y,dLdY,memory)devuelve las derivadasdLdXde la pérdida con respecto a la entrada de la capa, dondelayertiene una única entrada y una única salida.Ycorresponde a la salida de la función hacia delante ydLdYcorresponde a la derivada de la pérdida con respecto aY. La entradamemoryde la función corresponde a la salida de memoria de la función hacia delante.[dLdX,dLdW] = backward(layer,X,Y,dLdY,memory)también devuelve la derivadadLdWde la pérdida con respecto al parámetro que se puede aprender, dondelayertiene un único parámetro que se puede aprender.[dLdX,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory)también devuelve la derivadadLdSinde la pérdida con respecto a la entrada del estado, dondelayertiene un único parámetro de estado ydLdSoutcorresponde a la derivada de la pérdida con respecto a la salida de estado de la capa.[dLdX,dLdW,dLdSin] = backward(layer,X,Y,dLdY,dLdSout,memory)también devuelve la derivadadLdWde la pérdida con respecto al parámetro que se puede aprender y devuelve la derivadadLdSinde la pérdida con respecto a la entrada de estado de la capa, dondelayertiene un único parámetro de estado y un único parámetro que se puede aprender.
Puede ajustar las sintaxis para capas con varias entradas, varias salidas, varios parámetros que se pueden aprender o varios parámetros de estado:
Para capas con varias entradas, sustituya
XydLdXporX1,...,XNydLdX1,...,dLdXN, respectivamente, dondeNes el número de entradas.Para capas con varias salidas, sustituya
YydLdYporY1,...,YMydLdY1,...,dLdYM, respectivamente, dondeMes el número de salidas.Para capas con varios parámetros que se pueden aprender, sustituya
dLdWpordLdW1,...,dLdWP, dondePes el número de parámetros que se pueden aprender.Para capas con varios parámetros de estado, sustituya
dLdSinydLdSoutpordLdSin1,...,dLdSinKydLdSout1,...,dLdSoutK, respectivamente, dondeKes el número de parámetros de estado.
Para reducir el uso de memoria evitando que las variables que no se usan se guarden entre el paso hacia delante y el paso hacia atrás, sustituya los argumentos de entrada correspondientes por ~.
Sugerencia
Si el número de entradas a backward puede variar, use varargin después de layer, en lugar de los argumentos de entrada. En este caso, varargin es un arreglo de celdas de las entradas, donde los primeros N elementos corresponden a las N entradas de la capa, los siguientes M elementos corresponden a las M salidas de la capa, los siguientes M elementos corresponden a las derivadas de la pérdida con respecto a las M salidas de la capa, los siguientes K elementos corresponden a las K derivadas de la pérdida con respecto a las K salidas de estado, y el último elemento corresponde a memory.
Si el número de salidas puede variar, use varargout en lugar de argumentos de salida. En este caso, varargout es un arreglo de celdas de las salidas, donde los primeros N elementos corresponden a las N derivadas de la pérdida con respecto a las N entradas de la capa, los siguientes P elementos corresponden a las derivadas de la pérdida con respecto a los P parámetros que se pueden aprender y los siguientes K elementos corresponden a las derivadas de la pérdida con respecto a las K entradas de estado.
Los valores de X e Y son los mismos que en las funciones hacia delante. Las dimensiones de dLdY son las mismas que las dimensiones de Y.
Las dimensiones y el tipo de datos de dLdX son los mismos que las dimensiones y el tipo de datos de X. Las dimensiones y los tipos de datos de dLdW son los mismos que las dimensiones y tipos de datos de W.
Para calcular las derivadas de la pérdida con respecto a los datos de entrada, puede usar la regla de la cadena con las derivadas de la pérdida con respecto a los datos de salida y las derivadas de los datos de salida con respecto a los datos de entrada:
Cuando se usa la función trainnet, la capa actualiza automáticamente los parámetros que se pueden aprender usando las derivadas dLdW durante el paso hacia atrás.
Para ver un ejemplo de cómo definir una función de retropropagación personalizada, consulte Specify Custom Layer Backward Function.
Las salidas de la función de retropropagación de la capa personalizada pueden ser de valor complejo. (desde R2024a) Usar gradientes de valor complejo puede dar lugar a parámetros complejos que se pueden aprender. Para entrenar modelos con parámetros que se pueden aprender de valor complejo, utilice la función trainnet con los solvers "sgdm" "adam" o "rmsprop", especificándolos con la función trainingOptions, o utilice un bucle de entrenamiento personalizado con las funciones sgdmupdate, adamupdate o rmspropupdate.
Antes de R2024a: Las salidas de la función de retropropagación de la capa personalizada no deben ser complejas. Si la función de retropropagación implica números complejos, convierta todas las salidas de la función de retropropagación en valores reales antes de devolverlas.
Compatibilidad con la GPU
Si las funciones hacia delante de la capa admiten objetos dlarray, la capa es compatible con la GPU. En caso contrario, para ser compatibles con la GPU, las funciones de la capa deben admitir entradas y devolver salidas de tipo gpuArray (Parallel Computing Toolbox).
Muchas funciones integradas de MATLAB® admiten argumentos de entrada gpuArray (Parallel Computing Toolbox) y dlarray. Para obtener una lista de las funciones que admiten objetos dlarray, consulte List of Functions with dlarray Support. Para obtener una lista de las funciones que se ejecutan en una GPU, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox). Para utilizar una GPU para deep learning, debe también disponer de un dispositivo GPU compatible. Para obtener información sobre los dispositivos compatibles, consulte GPU Computing Requirements (Parallel Computing Toolbox). Para obtener más información sobre cómo trabajar con GPU en MATLAB, consulte Computación GPU en MATLAB (Parallel Computing Toolbox).
Compatibilidad con la generación de código
Debe especificar el pragma %#codegen en la definición de la capa para crear una capa personalizada para la generación de código. La generación de código no admite capas personalizadas con propiedades de estado (propiedades con atributo State).
Además, cuando genere código que usa bibliotecas de terceros:
La generación de código solo admite capas personalizadas con entradas de imágenes 2D o características.
Las entradas y la salida de las funciones hacia delante de la capa deben tener el mismo tamaño de lote.
Las propiedades no escalares deben ser un arreglo simple, doble o de caracteres.
Las propiedades escalares deben ser de tipo numérico, lógico o cadena.
Para ver un ejemplo de cómo crear una capa personalizada que admita la generación de código, consulte Define Custom Deep Learning Layer for Code Generation.
Composición de red
Para crear una capa personalizada que defina por sí misma una red neuronal, puede declarar un objeto dlnetwork como parámetro que se puede aprender en la sección properties (Learnable) de la definición de la capa. Este método se conoce como composición de red. Puede usar la composición de red para lo siguiente:
Crear una red con estructuras de control, por ejemplo, una red con una sección que pueda cambiar dinámicamente en función de los datos de entrada.
Crear una red con bucles; por ejemplo, una red con secciones que retroalimenten la salida.
Implementar el reparto de pesos; por ejemplo, en redes en las que diferentes datos deben pasar por las mismas capas, como las redes neuronales gemelas o las redes generativas antagónicas (GAN).
En el caso de redes anidadas que tienen parámetros que se pueden aprender y parámetros de estado, como las redes con normalización de lotes o las capas LSTM, declare la red en la sección properties (Learnable, State) de la definición de la capa.
Comprobar la validez de una capa
Si crea una capa de deep learning personalizada, puede utilizar la función checkLayer para comprobar si es válida. La función comprueba la validez de las capas, la compatibilidad con la GPU, si los gradientes están correctamente definidos y la compatibilidad con la generación de código. Para comprobar si una capa es válida, ejecute el siguiente comando:
checkLayer(layer,layout)
layer es una instancia de la capa y layout es un objeto networkDataLayout que especifica los tamaños y formatos de datos válidos para las salidas de la capa. Para realizar una comprobación con varias observaciones, utilice la opción ObservationDimension. Para comprobar la compatibilidad con la generación de código, establezca la opción CheckCodegenCompatibility en 1 (true). Para entradas de gran tamaño, las comprobaciones de gradiente tardan más en ejecutarse. Para acelerar el proceso, especifique un tamaño de entrada válido más pequeño.Para obtener más información, consulte Check Custom Layer Validity.
Comprobar la validez de una capa personalizada usando checkLayer
Compruebe la validez de la capa personalizada sreluLayer.
La capa personalizada sreluLayer, que se adjunta a este ejemplo como archivo de apoyo, aplica la operación SReLU a los datos de entrada. Para acceder a esta capa, abra el ejemplo como un script en vivo.
Cree una instancia de la capa.
layer = sreluLayer;
Cree un objeto networkDataLayout que especifique el tamaño de entrada esperado y el formato de la entrada típica a la capa. Especifique un tamaño de entrada válido de [24 24 20 128], donde las dimensiones corresponden a la altura, anchura, número de canales y número de observaciones de la salida de la capa anterior. Especifique el formato como "SSCB" (espacial, espacial, canal, lote).
validInputSize = [24 24 20 128];
layout = networkDataLayout(validInputSize,"SSCB");Compruebe la validez de la capa con checkLayer.
checkLayer(layer,layout)
Skipping GPU tests. No compatible GPU device found. Skipping code generation compatibility tests. To check validity of the layer for code generation, specify the CheckCodegenCompatibility and ObservationDimension options. Running nnet.checklayer.TestLayerWithoutBackward .......... .......... Done nnet.checklayer.TestLayerWithoutBackward __________ Test Summary: 20 Passed, 0 Failed, 0 Incomplete, 14 Skipped. Time elapsed: 0.34657 seconds.
La función no detecta ningún problema con la capa.
Consulte también
trainnet | trainingOptions | dlnetwork | functionLayer | checkLayer | setLearnRateFactor | setL2Factor | getLearnRateFactor | getL2Factor | findPlaceholderLayers | replaceLayer | PlaceholderLayer | networkDataLayout
Temas
- Define Custom Deep Learning Layer with Learnable Parameters
- Define Custom Deep Learning Layer with Multiple Inputs
- Define Custom Deep Learning Layer with Formatted Inputs
- Define Custom Recurrent Deep Learning Layer
- Specify Custom Layer Backward Function
- Define Custom Deep Learning Layer for Code Generation
- Deep Learning Network Composition
- Define Nested Deep Learning Layer Using Network Composition
- Check Custom Layer Validity