fminbnd

Encontrar el mínimo local de una función de una única variable en un intervalo fijo

Sintaxis

x = fminbnd(fun,x1,x2)

x = fminbnd(fun,x1,x2,options)

x = fminbnd(problem)

[x,fval] = fminbnd(___)

[x,fval,exitflag] = fminbnd(___)

[x,fval,exitflag,output] = fminbnd(___)

Descripción

fminbnd es un minimizador unidimensional que encuentra un mínimo local para un problema especificado por

$$\underset{x}{\min }f(x)\text{ such that }{x}_1<x<x_2.$$

x, x₁ y x₂ son escalares finitos, y f (x) es una función que devuelve un escalar.

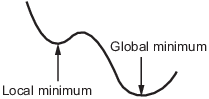
Si existen varios mínimos locales en el intervalo (x1,x2), fminbnd devuelve solo uno, que no se garantiza que sea el mínimo global. Para obtener más detalles, consulte Mínimo local frente a global.

x = fminbnd(fun,x1,x2) devuelve un valor x que es un minimizador local de la función de valor escalar que se describe en fun en el intervalo x1 < x < x2.

x = fminbnd(fun,x1,x2,options) minimiza con las opciones de optimización especificadas en options. Utilice optimset para establecer estas opciones.

x = fminbnd(problem) minimiza problem, donde problem es una estructura.

[x,fval] = fminbnd(___), para cualquier argumento de entrada, devuelve el valor de la función objetivo calculado en fun en la solución x.

[x,fval,exitflag] = fminbnd(___) también devuelve un valor exitflag que describe la condición de salida.

[x,fval,exitflag,output] = fminbnd(___) devuelve adicionalmente una estructura output que contiene información sobre la optimización.

Ejemplos

Mínimo de sin

Busque el punto en el que la función $$\sin (x)$$ alcanza a su mínimo en el intervalo $$0<x<2\pi$$.

fun = @sin;
x1 = 0;
x2 = 2*pi;
x = fminbnd(fun,x1,x2)

x = 
4.7124

Para mostrar la precisión, es igual que el valor correcto $$x=3\pi /2$$.

3*pi/2

ans = 
4.7124

Minimizar una función especificada por un archivo

Minimice una función especificada por un archivo de función independiente. Una función acepta un punto x y devuelve un escalar real que representa el valor de la función objetivo en x.

Escriba la siguiente función como un archivo y guárdelo como scalarobjective.m en su ruta de MATLAB®.

function f = scalarobjective(x)
f = 0;
for k = -10:10
    f = f + (k+1)^2*cos(k*x)*exp(-k^2/2);
end

Busque el valor x que minimiza scalarobjective en el intervalo 1 <= x <= 3.

x = fminbnd(@scalarobjective,1,3)

x =

    2.0061

Minimizar con un parámetro extra

Minimice una función cuando hay un parámetro extra. La función $$\sin (x-a)$$ tiene un valor mínimo que depende del valor del parámetro $$a$$. Cree una función anónima de $$x$$ que incluya el valor del parámetro $$a$$. Minimice esta función en el intervalo $$0<x<2\pi$$.

a = 9/7;
fun = @(x)sin(x-a);
x = fminbnd(fun,1,2*pi)

x = 
5.9981

Esta respuesta es correcta; el valor teórico es

3*pi/2 + 9/7

ans = 
5.9981

Para obtener más información sobre la inclusión de parámetros adicionales, consulte Parametrizar funciones.

Monitorizar las iteraciones

Monitorice los pasos que da fminbnd para minimizar la función $$\sin (x)$$ para $$0<x<2\pi$$.

fun = @sin;
x1 = 0;
x2 = 2*pi;
options = optimset('Display','iter');
x = fminbnd(fun,x1,x2,options)

 
 Func-count     x          f(x)         Procedure
    1        2.39996      0.67549        initial
    2        3.88322     -0.67549        golden
    3        4.79993    -0.996171        golden
    4        5.08984    -0.929607        parabolic
    5        4.70582    -0.999978        parabolic
    6         4.7118           -1        parabolic
    7        4.71239           -1        parabolic
    8        4.71236           -1        parabolic
    9        4.71242           -1        parabolic
 
Optimization terminated:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04 

x = 
4.7124

Encontrar la ubicación y el valor de la función de un mínimo

Encuentre la ubicación del mínimo de $$\sin (x)$$ y el valor del mínimo para $$0<x<2\pi$$.

fun = @sin;
[x,fval] = fminbnd(fun,1,2*pi)

x = 
4.7124

fval = 
-1.0000

Obtener toda la información

Devuelva toda la información sobre el proceso de solución de fminbnd solicitando todas las salidas. Además, monitorice el proceso de solución utilizando una función de gráfica.

fun = @sin;
x1 = 0;
x2 = 2*pi;
options = optimset('PlotFcns',@optimplotfval);
[x,fval,exitflag,output] = fminbnd(fun,x1,x2,options)

x = 
4.7124

fval = 
-1.0000

exitflag = 
1

output = struct with fields:
    iterations: 8
     funcCount: 9
     algorithm: 'golden section search, parabolic interpolation'
       message: 'Optimization terminated:↵ the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04 ↵'

Argumentos de entrada

fun — Función que se desea minimizar

identificador de función | nombre de función

Función que se desea minimizar, especificada como un identificador de función o nombre de función. fun es una función que acepta un escalar real x y devuelve un escalar real f (la función objetivo evaluada en x).

Especifique fun como un identificador de función para un archivo:

x = fminbnd(@myfun,x1,x2)

donde myfun es una función de MATLAB^® como

function f = myfun(x)
f = ...            % Compute function value at x

También puede especificar fun como un identificador de función para una función anónima:

x = fminbnd(@(x)norm(x)^2,x1,x2);

Ejemplo: fun = @(x)-x*exp(-3*x)

Tipos de datos: char | function_handle | string

x1 — Límite inferior

escalar real finito

Límite inferior, especificado como un escalar real finito.

Ejemplo: x1 = -3

Tipos de datos: double

x2 — Límite superior

escalar real finito

Límite superior, especificado como un escalar real finito.

Ejemplo: x2 = 5

Tipos de datos: double

options — Opciones de optimización

estructura como la que optimset devuelve

Opciones de optimización, especificadas como una estructura como la que optimset devuelve. Puede utilizar optimset para establecer o cambiar los valores de estos campos en la estructura de opciones. Para obtener información detallada, consulte Establecer opciones de optimización.

Display	Nivel de visualización (consulte Optimization Solver Iterative Display): 'notify' (valor predeterminado) muestra la salida solo si la función no converge. 'off' o 'none' no muestran la salida. 'iter' muestra la salida en cada iteración. 'final' muestra solo la salida final.
FunValCheck	Comprobar si los valores de la función objetivo son válidos. El valor predeterminado 'off' permite que fminbnd actúe cuando la función objetivo devuelve un valor complex o NaN. La configuración 'on' genera un error cuando la función objetivo devuelve un valor complex o NaN.
MaxFunEvals	Número máximo de evaluaciones de función permitidas, un entero positivo. El valor predeterminado es 500. Consulte Tolerancias y criterios de parada.
MaxIter	Número máximo de iteraciones permitidas, un entero positivo. El valor predeterminado es 500. Consulte Tolerancias y criterios de parada.
OutputFcn	Especificar una o más funciones definidas por el usuario a las que una función de optimización llama en cada iteración, ya sea como identificador de función o como arreglo de celdas de identificadores de función. El valor predeterminado es ninguno []. Consulte Optimization Solver Output Functions.
PlotFcns	Representar varias medidas de progreso mientras se ejecuta el algoritmo. Seleccione desde las gráficas predefinidas o cree la suya. Pase un nombre o identificador de función o un arreglo de celdas de nombres o identificadores de función. El valor predeterminado es ninguno ([]): @optimplotx representa el punto actual @optimplotfunccount representa el recuento de la función @optimplotfval representa el valor de la función Para obtener más información sobre cómo escribir una función de representación gráfica personalizada, consulte Optimization Solver Plot Functions.
TolX	Tolerancia de terminación en x, un escalar positivo. El valor predeterminado es 1e-4. Consulte Tolerancias y criterios de parada.

Ejemplo: options = optimset('Display','iter')

Tipos de datos: struct

problem — Estructura de problema

estructura

Estructura de problema, especificada como una estructura con los campos siguientes.

Nombre de campo	Entrada
objective	Función objetivo
x1	Punto final izquierdo
x2	Punto final derecho
solver	'fminbnd'
options	Estructura de opciones como la devuelta por optimset

Tipos de datos: struct

Argumentos de salida

x — Solución

escalar real

Solución, devuelta como un escalar real. Habitualmente, x es una solución local al problema cuando exitflag es positivo. Consulte Mínimo local frente a global.

fval — Valor de función objetivo en la solución

número real

Valor de función objetivo en la solución, devuelto como número real. Por lo general, fval = fun(x).

exitflag — Razón por la que fminbnd se ha detenido

valor entero

Razón por la que fminbnd se ha detenido, devuelta como entero.

1	La función no convergió en una solución x.
0	El número de iteraciones excedió options.MaxIter o el número de evaluaciones de función excedió options.MaxFunEvals.
-1	Detenido por una función de salida o una función de gráfica.
-2	Los límites son incoherentes, por lo que x1 > x2.

output — Información sobre el proceso de optimización

estructura

Información sobre el proceso de optimización, devuelto como estructura con campos:

iterations	Número de iteraciones realizadas
funcCount	Número de evaluaciones de función
algorithm	'golden section search, parabolic interpolation'
message	Mensaje de salida

Limitaciones

• La función que desea minimizar debe ser continua.

• fminbnd puede que solo ofrezca soluciones locales.

• fminbnd puede mostrar una convergencia lenta cuando la solución se encuentra en un límite del intervalo.

Más acerca de

Mínimo local frente a global

En general, los solvers de optimización devuelven un mínimo local (u óptimo). El resultado puede ser un mínimo global (u óptimo), pero puede no serlo.

• Un mínimo local de una función es un punto en el que el valor de la función es menor que en puntos cercanos, pero posiblemente mayor que en un punto lejano.

• Un mínimo global de una función es un punto en el que el valor de la función es menor que en todos los demás puntos factibles.

Los solvers de optimización de MATLAB y Optimization Toolbox™ suelen devolver un mínimo local. Los solvers de Global Optimization Toolbox pueden buscar un mínimo global, pero no garantizan que sus soluciones sean globales. Consulte Find Global or Multiple Local Minima (Global Optimization Toolbox) para ver un ejemplo de búsqueda global.

Algoritmos

fminbnd es un archivo de función. El algoritmo se basa en la búsqueda de la sección áurea y la interpolación parabólica. A menos que el punto final izquierdo x₁ esté muy cerca del punto final derecho x₂, fminbnd nunca evalúa fun en los puntos finales, por lo que fun solo debe definirse para x en el intervalo x₁ < x < x₂.

Si el mínimo se produce realmente en x₁ o x₂, fminbnd devuelve un punto x en el interior del intervalo (x₁, x₂) que está cerca del minimizador. En este caso, la distancia de x respecto al minimizador no es superior a 2*(TolX + 3*abs(x)*sqrt(eps)). Consulte [1] o [2] para obtener información sobre el algoritmo.

Funcionalidad alternativa

App

La tarea Optimize de Live Editor proporciona una interfaz visual para fminbnd.

Referencias

[1] Forsythe, G. E., M. A. Malcolm, and C. B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice Hall, 1976.

[2] Brent, Richard. P. Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.

Capacidades ampliadas

Generación de código C/C++

Genere código C y C++ mediante MATLAB® Coder™.

Para generación de código C/C++:

• fminbnd no admite el argumento de la estructura del problema.

• fminbnd ignora la opción Display y no muestra la visualización iterativa ni un mensaje de salida. Para comprobar la calidad de la solución, examine el indicador de salida.

• La estructura de salida no incluye los campos algorithm o message.

• fminbnd ignora las opciones OutputFcn y PlotFcns.

Entorno basado en subprocesos

Ejecute código en segundo plano con MATLAB® backgroundPool o acelere código con Parallel Computing Toolbox™ ThreadPool.

Esta función es totalmente compatible con entornos basados en subprocesos. Para obtener más información, consulte Ejecutar funciones de MATLAB en entornos basados en subprocesos.

Historial de versiones

Introducido antes de R2006a

Consulte también

fminsearch | fzero | optimset | Optimize

Temas

• Minimizar funciones de una variable
• Crear un identificador de función
• Funciones anónimas