mink
Find k smallest elements of array
Description
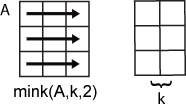
B = mink(A,k)k smallest elements of A.
If
Ais a vector, thenminkreturns a vector containing theksmallest elements ofA.If
Ais a matrix, thenminkreturns a matrix whose columns contain theksmallest elements of each column ofA.If
Ais a multidimensional array, thenminkreturns theksmallest elements along the first dimension whose size does not equal 1.