La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Planificar una ruta para un robot de bicicleta en Simulink

Este ejemplo muestra cómo ejecutar una ruta libre de obstáculos entre dos ubicaciones de un determinado mapa en Simulink®. La ruta se genera mediante un algoritmo de planificación de rutas probabilísticas (PRM) (mobileRobotPRM)). Los controles de comando para desplazarse por esta ruta se generan utilizando el bloque de controlador Pure Pursuit. Un modelo de movimiento cinemático de bicicleta simula el movimiento del robot a partir de estos comandos.

Cargar el mapa y el modelo de Simulink

Cargue el mapa en el área de trabajo de MATLAB

load exampleMaps.mat

Introduzca las ubicaciones inicial y objetivo

startLoc = [5 5];
goalLoc = [12 3];

Los mapas importados son: simpleMap, complexMap y ternaryMap.

Abra el modelo de Simulink

open_system('pathPlanningBicycleSimulinkModel.slx')

Visión general del modelo

El modelo se compone de cuatro operaciones primarias:

• Planificación

• Control

• Modelo de planta

Planificación

El bloque de función de MATLAB® Planner utiliza el planificador de rutas mobileRobotPRM y toma como entradas una ubicación inicial, una ubicación objetivo y un mapa. Los bloques generan el arreglo de waypoints que sigue el robot. Posteriormente, los waypoints planificados son usados por el bloque de controlador Pure Pursuit.

Control

Pure Pursuit

El bloque de controlador Pure Pursuit genera los comandos de velocidad lineal y angular en función de los waypoints y la pose actual del robot.

Comprobar si se alcanza el objetivo

El subsistema Check Distance to Goal calcula la distancia actual hasta el objetivo y, si se encuentra dentro de un umbral, la simulación se detiene.

Modelo de planta

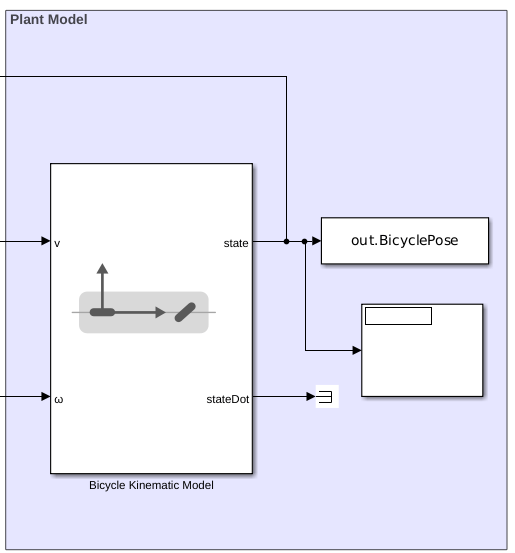
El bloque Bicycle Kinematic Model crea un modelo de vehículo para simular la cinemática simplificada de un vehículo. El bloque toma velocidades lineales y angulares como entradas de comando desde el bloque de controlador Pure Pursuit y genera los estados de posición y velocidad actuales.

Ejecutar el modelo

Para simular el modelo

simulation = sim('pathPlanningBicycleSimulinkModel.slx');

Visualizar el movimiento del robot

Para ver las poses:

map = binaryOccupancyMap(simpleMap)

map = 
  binaryOccupancyMap with properties:

   mapLayer Properties
              LayerName: 'binaryLayer'
               DataType: 'logical'
           DefaultValue: 0
    GridLocationInWorld: [0 0]
      GridOriginInLocal: [0 0]
     LocalOriginInWorld: [0 0]
             Resolution: 1
               GridSize: [26 27]
           XLocalLimits: [0 27]
           YLocalLimits: [0 26]
           XWorldLimits: [0 27]
           YWorldLimits: [0 26]

robotPose = simulation.BicyclePose

robotPose = 362×3

    5.0000    5.0000         0
    5.0001    5.0000   -0.0002
    5.0007    5.0000   -0.0012
    5.0036    5.0000   -0.0062
    5.0181    4.9997   -0.0313
    5.0902    4.9929   -0.1569
    5.4081    4.8311   -0.7849
    5.5189    4.6758   -1.1170
    5.5366    4.6356   -1.1930
    5.5512    4.5942   -1.2684
      ⋮

numRobots = size(robotPose, 2) / 3;
thetaIdx = 3;

% Translation
xyz = robotPose;
xyz(:, thetaIdx) = 0;

% Rotation in XYZ euler angles
theta = robotPose(:,thetaIdx);
thetaEuler = zeros(size(robotPose, 1), 3 * size(theta, 2));
thetaEuler(:, end) = theta;

for k = 1:size(xyz, 1)
    show(map)
    hold on;
    
    % Plot Start Location
    plotTransforms([startLoc, 0], eul2quat([0, 0, 0]))
    text(startLoc(1), startLoc(2), 2, 'Start');
    
    % Plot Goal Location
    plotTransforms([goalLoc, 0], eul2quat([0, 0, 0]))
    text(goalLoc(1), goalLoc(2), 2, 'Goal');
    
    % Plot Robot's XY locations
    plot(robotPose(:, 1), robotPose(:, 2), '-b')
    
    % Plot Robot's pose as it traverses the path
    quat = eul2quat(thetaEuler(k, :), 'xyz');
    plotTransforms(xyz(k,:), quat, 'MeshFilePath',...
        'groundvehicle.stl');
    
    pause(0.01)
    hold off;
end

© Copyright 2019-2020 The MathWorks, Inc.