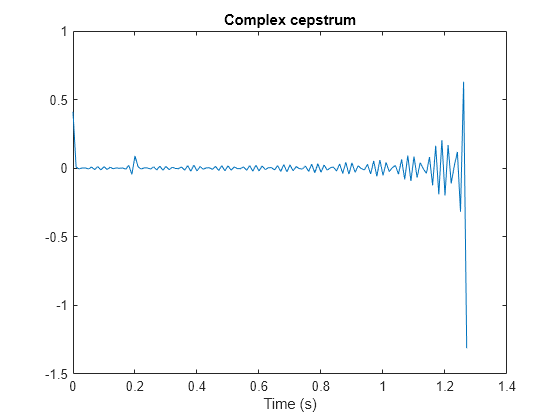
cceps

Complex cepstral analysis

Syntax

xhat = cceps(x)

[xhat,nd] = cceps(x)

[xhat,nd,xhat1] = cceps(x)

[___] = cceps(x,n)

Description

xhat = cceps(x) returns the complex cepstrum xhat of the real data sequence x using the Fourier transform.

Note

cceps only works on real data.

[xhat,nd] = cceps(x) returns the number of samples nd of (circular) delay added to x prior to finding the complex cepstrum.

[xhat,nd,xhat1] = cceps(x) returns a second complex cepstrum, xhat1.

[___] = cceps(x,n) zero pads x to length n and returns the length n.

Examples

Using cceps to show an echo

This example uses cceps to show an echo. Generate a sine of frequency 45 Hz, sampled at 100 Hz. Add an echo with half the amplitude and 0.2 s later. Compute the complex cepstrum of the signal. Notice the echo at 0.2 s.

Fs = 100;
t = 0:1/Fs:1.27;

s1 = sin(2*pi*45*t);		
s2 = s1 + 0.5*[zeros(1,20) s1(1:108)];

c = cceps(s2);

plot(t,c)
xlabel('Time (s)')
title('Complex cepstrum')

Input Arguments

x — Input signal

real vector

Input signal, specified as a real vector. By the application of a linear phase term, the input is altered to have no phase discontinuity at ±π radians. That is, it is circularly shifted (after zero padding) by some samples, if necessary, to have zero phase at π radians.

n — Length of zero-padded signal

positive real integer

Length of zero-padded signal, specified as a positive real integer.

Output Arguments

xhat — Complex cepstrum

vector

Complex cepstrum, returned as a vector.

nd — Number of samples

real positive scalar

Number of samples of circular delay added to x, returned as a positive real scalar.

xhat1 — Second complex cepstrum

vector

Second complex cepstrum, returned as a vector. xhat1 is computed using an alternative factorization algorithm specified in the references [1] and [2]. This method can be applied only to finite-duration signals. See the Algorithm section below for a comparison of the Fourier and factorization methods of computing the complex cepstrum.

Algorithms

Cepstral analysis is a nonlinear signal processing technique that is applied most commonly in speech processing and homomorphic filtering [1]. cceps is an implementation of algorithm 7.1 in [3]. A lengthy Fortran program reduces to these three lines of MATLAB^® code, which compose the core of cceps:

h = fft(x);
logh = log(abs(h)) + sqrt(-1)*rcunwrap(angle(h));
y = real(ifft(logh));

Note

rcunwrap in the above code segment is a special version of unwrap that subtracts a straight line from the phase. rcunwrap is a local function within cceps and is not available for use from the MATLAB command line.

The following table lists the pros and cons of the Fourier and factorization algorithms.

Algorithm	Pros	Cons
Fourier	Can be used for any signal.	Requires phase unwrapping. Output is aliased.
Factorization	Does not require phase unwrapping. No aliasing	Can be used only for short duration signals. Input signal must have an all-zero Z-transform with no zeros on the unit circle.

In general, you cannot use the results of these two algorithms to verify each other. You can use them to verify each other only when the first element of the input data is positive, the Z-transform of the data sequence has only zeros, all of these zeros are inside the unit circle, and the input data sequence is long (or padded with zeros).

References

[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, pp. 788–789.

[2] Steiglitz, K., and B. Dickinson. “Computation of the Complex Cepstrum by Factorization of the Z-transform.” Proceedings of the 1977 IEEE^® International Conference on Acoustics, Speech and Signal Processing, pp. 723–726.

[3] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced before R2006a