La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Señal analítica de un coseno

Este ejemplo muestra cómo determinar la señal analítica. El ejemplo también demuestra que la parte imaginaria de la señal analítica que corresponde a un coseno es un seno con la misma frecuencia. Si el coseno tiene una media distinta de cero (desplazamiento de CC), la parte real de la señal analítica es el coseno original con la misma media, pero la parte imaginaria tiene media cero.

Cree un coseno con una frecuencia de 100 Hz. La tasa de muestreo es 10 kHz. Añada un desplazamiento de CC de 2,5 al coseno.

t = 0:1e-4:1;
x = 2.5 + cos(2*pi*100*t);

Utilice la función hilbert para obtener la señal analítica. La parte real es igual a la señal original. La parte imaginaria es la transformada de Hilbert de la señal original. Represente las partes real e imaginaria para compararlas.

y = hilbert(x);

plot(t,real(y))
hold on
plot(t,imag(y))
xlim([0 0.1])
grid on
text([0.015 0.015],[3.7 1.2], ...
    {'Real Part \downarrow';'Imaginary Part \downarrow'})

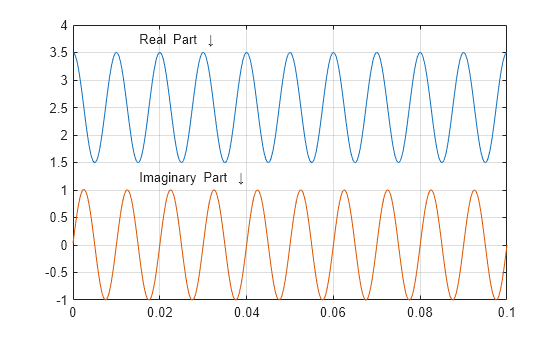
Puede ver que la parte imaginaria es un seno con la misma frecuencia que la parte real del coseno. Sin embargo, la parte imaginaria tiene una media de cero, mientras que la parte real tiene una media de 2,5.

La señal original es

$$x(t)=2.5+\cos (2\pi 1000t).$$

La señal analítica resultante es

$$z(t)=2.5+e^{j2\pi 1000t}.$$

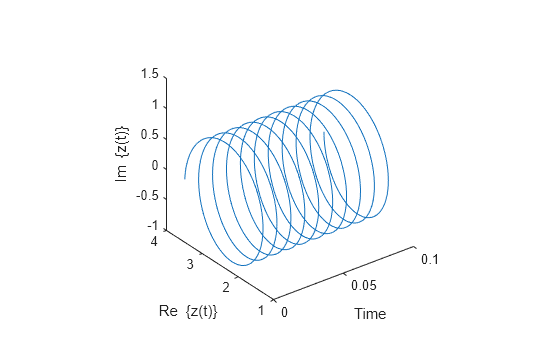
Represente 10 periodos de la señal analítica de valor complejo.

prds = 1:1000;

figure
plot3(t(prds),real(y(prds)),imag(y(prds)))

xlabel('Time')
ylabel('Re \{z(t)\}')
zlabel('Im \{z(t)\}')
axis square

Consulte también

hilbert