Transformada de Hilbert y frecuencia instantánea
La transformada de Hilbert calcula la frecuencia instantánea de una señal solo para señales monocomponente. Una señal monocomponente se describe en el plano tiempo-frecuencia con una sola "cresta". El conjunto de señales monocomponente incluye sinusoides sencillas y señales como chirps.
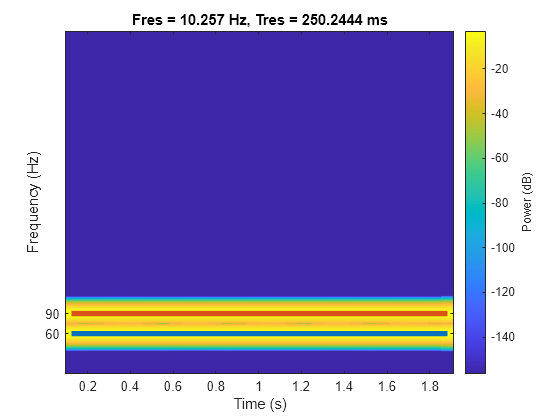
Genere un chirp muestreado a 1 kHz durante dos segundos. Especifique el chirp para que su frecuencia sea inicialmente 100 Hz y aumente a 200 Hz al pasar un segundo.
fs = 1000; t = 0:1/fs:2-1/fs; y = chirp(t,100,1,200);
Calcule el espectrograma del chirp utilizando la transformada de Fourier de tiempo corto implementada en la función pspectrum. La señal está bien descrita por una frecuencia de pico simple en cada punto en el tiempo.
pspectrum(y,fs,'spectrogram')
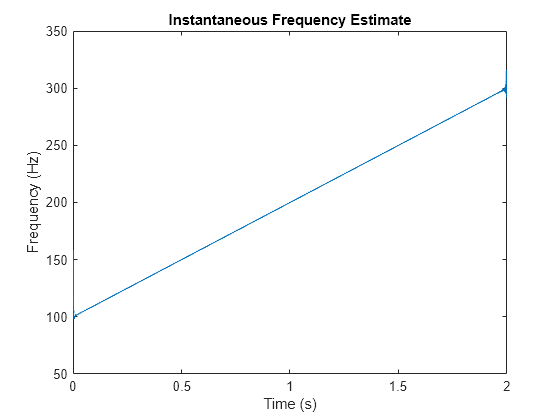
Calcule la señal analítica y diferencie su fase para medir la frecuencia instantánea. La derivada escalada produce un cálculo significativo.
z = hilbert(y); instfrq = fs/(2*pi)*diff(unwrap(angle(z))); clf plot(t(2:end),instfrq) ylim([0 fs/2])

La función instfreq calcula y muestra la frecuencia instantánea en un paso.
instfreq(y,fs,'Method','hilbert')
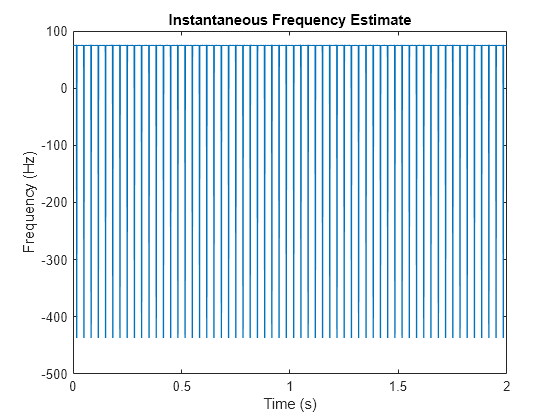
El método falla cuando la señal no es monocomponente.
Genere una suma de dos sinusoides de 60 Hz y 90 Hz de frecuencia, muestreadas a 1023 Hz durante dos segundos. Calcule y represente el espectrograma. Cada punto de tiempo muestra la presencia de los dos componentes.
fs = 1023;
t = 0:1/fs:2-1/fs;
x = sin(2*pi*60*t)+sin(2*pi*90*t);
pspectrum(x,fs,'spectrogram')
yticks([60 90])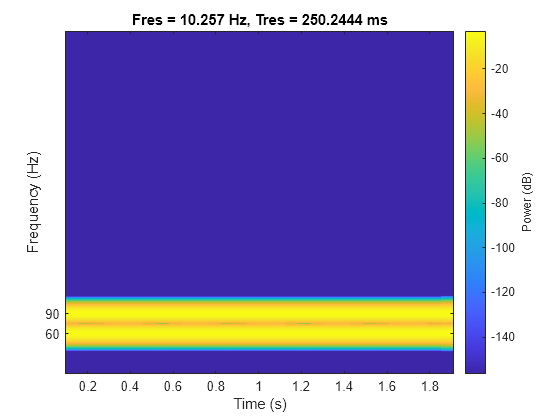
Calcule la señal analítica y diferencie su fase. Amplíe el zoom en la región que contiene las frecuencias de las sinusoides. La señal analítica predice una frecuencia instantánea que es la media de las frecuencias de las sinusoides.
z = hilbert(x); instfrq = fs/(2*pi)*diff(unwrap(angle(z))); plot(t(2:end),instfrq) ylim([60 90]) xlabel('Time (s)') ylabel('Frequency (Hz)')

La función instfreq también calcula la media.
instfreq(x,fs,'Method','hilbert')
Para calcular ambas frecuencias como funciones de tiempo, utilice spectrogram para encontrar la densidad del espectro de potencia y tfridge para realizar un seguimiento de las dos crestas. En tfridge, especifique la penalización para cambiar la frecuencia a 0,1.
[s,f,tt] = pspectrum(x,fs,'spectrogram'); numcomp = 2; [fridge,~,lr] = tfridge(s,f,0.1,'NumRidges',numcomp); pspectrum(x,fs,'spectrogram') hold on plot3(tt,fridge,abs(s(lr)),'LineWidth',4) hold off yticks([60 90])