coefCI

Confidence intervals for coefficient estimates of multinomial regression model

Since R2023a

Syntax

ci = coefCI(mdl)

ci = coefCI(mdl,alpha)

Description

ci = coefCI(mdl) returns 95% confidence intervals for the coefficients in mdl.

ci = coefCI(mdl,alpha) returns the confidence intervals using the confidence level 100(1 – alpha)%.

Examples

Find Confidence Intervals for Model Coefficients

Load the carbig data set.

load carbig

The variables Horsepower, Weight, and Origin contain data for car horsepower, weight, and country of origin, respectively. The variable MPG contains car mileage data.

Create a table in which the Origin and MPG variables are categorical.

Origin = categorical(cellstr(Origin));
MPG = discretize(MPG,[9 19 29 39 48],"categorical");
tbl = table(Horsepower,Weight,Origin,MPG);

Fit a multinomial regression model. Specify Horsepower, Weight, and Origin as predictor variables, and specify MPG as the response variable.

modelspec = "MPG ~ 1 + Horsepower + Weight + Origin";
mdl = fitmnr(tbl,modelspec);

Find the 95% confidence intervals for the coefficients. Display the coefficient names and confidence intervals in a table by using the array2table function.

ci = coefCI(mdl);
ciTable = array2table(ci, ...
    RowNames = mdl.Coefficients.Properties.RowNames, ...
    VariableNames = ["LowerLimit","UpperLimit"])

ciTable=27×2 table
                               LowerLimit     UpperLimit
                               ___________    __________

    (Intercept_[9, 19))            -89.395       32.927 
    Horsepower_[9, 19)             0.14928      0.27499 
    Weight_[9, 19)               0.0022537    0.0069061 
    Origin_France_[9, 19)          -54.498       69.362 
    Origin_Germany_[9, 19)         -62.237       59.666 
    Origin_Italy_[9, 19)           -73.457        54.35 
    Origin_Japan_[9, 19)           -62.743       59.097 
    Origin_Sweden_[9, 19)          -60.076       63.853 
    Origin_USA_[9, 19)             -59.875       61.926 
    (Intercept_[19, 29))           -78.671       43.544 
    Horsepower_[19, 29)            0.12131      0.24115 
    Weight_[19, 29)            -0.00073846    0.0033281 
    Origin_France_[19, 29)         -49.929       73.841 
    Origin_Germany_[19, 29)        -57.315       64.476 
    Origin_Italy_[19, 29)          -51.881       73.071 
    Origin_Japan_[19, 29)           -58.22       63.559 
      ⋮

Each row contains the lower and upper limits for the 95% confidence intervals.

Specify Confidence Level

Load the carbig data set.

load carbig

The variables Horsepower, Weight, and Origin contain data for car horsepower, weight, and country of origin. The variable MPG contains car mileage data.

Create a table in which the Origin and MPG variables are categorical.

Origin = categorical(cellstr(Origin));
MPG = discretize(MPG,[9 19 29 39 48],"categorical");
tbl = table(Horsepower,Weight,Origin,MPG);

Fit a multinomial regression model. Specify Horsepower, Weight, and Origin as predictor variables, and specify MPG as the response variable.

modelspec = "MPG ~ 1 + Horsepower + Weight + Origin";
mdl = fitmnr(tbl,modelspec);

Find the 95% and 99% confidence intervals for the coefficients. Display the coefficient names and confidence intervals in a table by using the array2table function.

ci95 = coefCI(mdl);
ci99 = coefCI(mdl,0.01);
confIntervals = array2table([ci95 ci99], ...
    RowNames=mdl.Coefficients.Properties.RowNames, ...
    VariableNames=["95LowerLimit","95UpperLimit", ...
    "99LowerLimit","99UpperLimit"])

confIntervals=27×4 table
                               95LowerLimit    95UpperLimit    99LowerLimit    99UpperLimit
                               ____________    ____________    ____________    ____________

    (Intercept_[9, 19))            -89.395         32.927         -108.66          52.194  
    Horsepower_[9, 19)             0.14928        0.27499         0.12948         0.29478  
    Weight_[9, 19)               0.0022537      0.0069061       0.0015209       0.0076389  
    Origin_France_[9, 19)          -54.498         69.362         -74.007          88.871  
    Origin_Germany_[9, 19)         -62.237         59.666         -81.438          78.868  
    Origin_Italy_[9, 19)           -73.457          54.35         -93.588          74.481  
    Origin_Japan_[9, 19)           -62.743         59.097         -81.935          78.288  
    Origin_Sweden_[9, 19)          -60.076         63.853         -79.596          83.373  
    Origin_USA_[9, 19)             -59.875         61.926          -79.06          81.111  
    (Intercept_[19, 29))           -78.671         43.544         -97.921          62.794  
    Horsepower_[19, 29)            0.12131        0.24115         0.10243         0.26003  
    Weight_[19, 29)            -0.00073846      0.0033281       -0.001379       0.0039687  
    Origin_France_[19, 29)         -49.929         73.841         -69.424          93.336  
    Origin_Germany_[19, 29)        -57.315         64.476         -76.498          83.659  
    Origin_Italy_[19, 29)          -51.881         73.071         -71.563          92.752  
    Origin_Japan_[19, 29)           -58.22         63.559         -77.401           82.74  
      ⋮

Each row contains the lower and upper limits for the 95% and 99% confidence intervals.

Visualize the confidence intervals by plotting their limits with the coefficient values.

ci95 = coefCI(mdl);
ci99 = coefCI(mdl,0.01);
colors = lines(3);
hold on
p = plot(mdl.Coefficients.Value,Color=colors(1,:));
plot(ci95(:,1),Color=colors(2,:),LineStyle="--")
plot(ci95(:,2),Color=colors(2,:),LineStyle="--")
plot(ci99(:,1),Color=colors(3,:),LineStyle="--")
plot(ci99(:,2),Color=colors(3,:),LineStyle="--")
hold off
legend(["Coefficients","95% CI","","99% CI",""], ...
    Location="southeast")

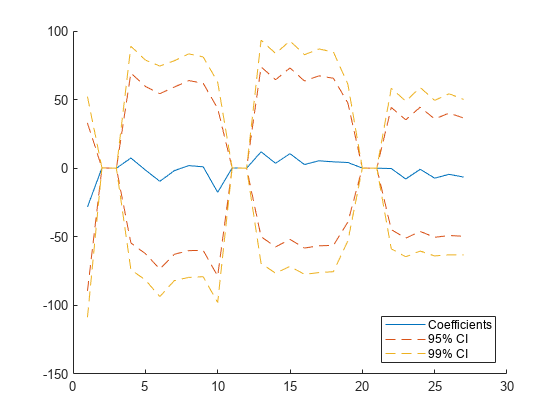
The plot shows that the 99% confidence intervals for the coefficients are wider than the 95% confidence intervals.

Input Arguments

mdl — Multinomial regression model object

MultinomialRegression model object

Multinomial regression model object, specified as a MultinomialRegression model object created with the fitmnr function.

alpha — Significance level

0.05 (default) | numeric value in the range [0,1]

Significance level for the confidence interval, specified as a numeric value in the range [0,1]. The confidence level of ci is equal to 100(1 – alpha)%. alpha is the probability that the confidence interval does not contain the true value.

Example: 0.01

Data Types: single | double

Output Arguments

ci — Confidence intervals

numeric matrix

Confidence intervals, returned as a p-by-2 numeric matrix, where p is the number of coefficients. The jth row of ci is the confidence interval for the jth coefficient of mdl. The name of coefficient j is stored in the CoefficientNames property of mdl.

More About

Confidence Intervals

The coefficient confidence intervals provide a measure of precision for regression coefficient estimates.

A 100(1 – α)% confidence interval gives the range for the corresponding regression coefficient with 100(1 – α)% confidence, meaning that 100(1 – α)% of the intervals resulting from repeated experimentation will contain the true value of the coefficient.

The software finds confidence intervals using the Wald method. The 100(1 – α)% confidence intervals for regression coefficients are

$$b_i\pm t_{\left(1-\alpha /2,n-p\right)}SE\left(b_i\right),$$

where b_i is the coefficient estimate, SE(b_i) is the standard error of the coefficient estimate, and t_{(1–α/2,n–p)} is the 100(1 – α/2) percentile of the t-distribution with n – p degrees of freedom. n is the number of observations and p is the number of regression coefficients.

Version History

Introduced in R2023a