bboxresize
Resize bounding boxes
Description
Examples
Read an image.
I = imread('peppers.png');Define bounding boxes and labels.
bboxA = [
410 230 100 90
186 78 80 60
]bboxA = 2×4
410 230 100 90
186 78 80 60
labelsA = [
"garlic"
"onion"
];Resize the image and the bounding boxes.
scale = 1.5; J = imresize(I,scale); bboxB = bboxresize(bboxA,scale);
Display the results.
figure I = insertObjectAnnotation(I,'Rectangle',bboxA,labelsA); J = insertObjectAnnotation(J,'Rectangle',bboxB,labelsA); imshowpair(I,J,'montage')

Input Arguments
Bounding boxes, specified as an M-by-4, M-by-5, or M-by-9 nonsparse numeric matrix of M bounding boxes. Each row, M, of the matrix defines a bounding box as either an axis-aligned rectangle, a rotate rectangle, or a cuboid. The table below describes the format of the bounding boxes.
| Bounding Box | Description |
|---|---|
| Axis-aligned rectangle |
Defined in spatial coordinates as an M-by-4 numeric matrix with rows of the form [x y w h], where:
|
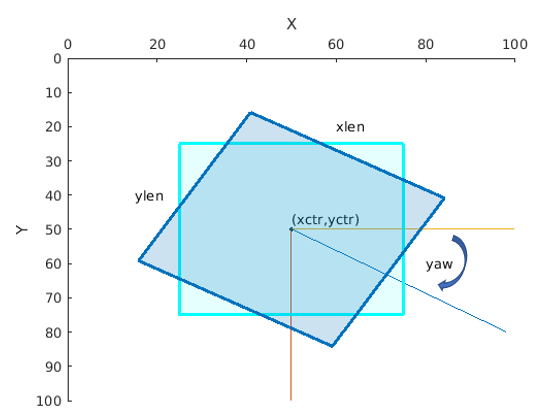
| Rotated rectangle |
Defined in spatial coordinates as an M-by-5 numeric matrix with rows of the form [xctr yctr xlen ylen yaw], where:
|
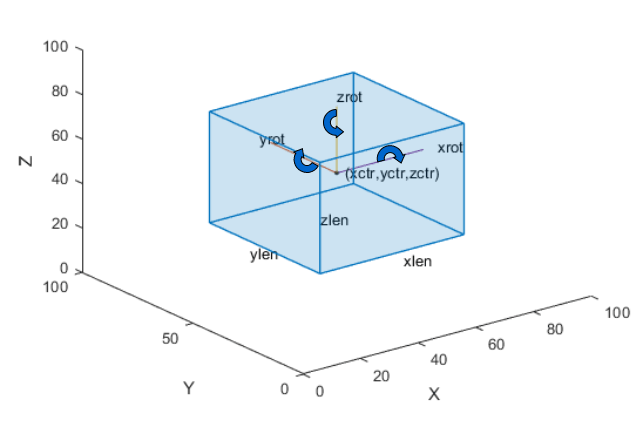
| Cuboid |
Defined in spatial coordinates as an M-by-9 numeric matrix with rows of the form [xctr yctr zctr xlen ylen zlen xrot yrot zrot], where:
The figure shows how these values determine the position of a cuboid.
|
Scale, specified as a scalar or a row vector. When you specify a scalar, the
function applies the same scale factor to the height and width of the bounding boxes in
bboxA. When you specify a row vector, the function applies the
factor in the first element of the vector to resize the height and the second element to
resize the width of the bounding boxes.
Output Arguments
Warped bounding boxes, returned as an M2-by-N
matrix of M2 bounding boxes. The number of bounding boxes returned is
less than the number of bounding boxes in the input. Each row, M2, of
the matrix defines one bounding box of the same type as the input
bboxA. When bboxB contains floating point
data, the function returns it with the same type as bboxA.
Otherwise, the function returns bboxB as type
single.
Version History
Introduced in R2019bThe bboxresize,
bboxcrop,
bboxwarp, and
showShape
functions assume the input bounding box coordinates for axis-aligned rectangles are
specified in spatial coordinates and return the transformed bounding boxes in spatial
coordinates.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)