Train Wasserstein GAN with Gradient Penalty (WGAN-GP)

This example shows how to train a Wasserstein generative adversarial network with a gradient penalty (WGAN-GP) to generate images.

A generative adversarial network (GAN) is a type of deep learning network that can generate data with similar characteristics as the input real data.

A GAN consists of two networks that train together:

1. Generator — Given a vector of random values (latent inputs) as input, this network generates data with the same structure as the training data.

2. Discriminator — Given batches of data containing observations from both the training data, and generated data from the generator, this network attempts to classify the observations as "real" or "generated".

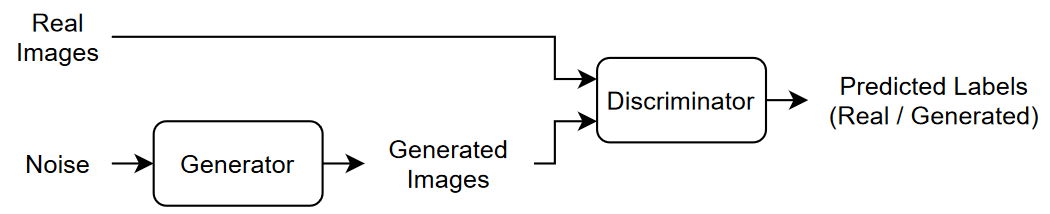
To train a GAN, train both networks simultaneously to maximize the performance of both:

• Train the generator to generate data that "fools" the discriminator.

• Train the discriminator to distinguish between real and generated data.

To optimize the performance of the generator, maximize the loss of the discriminator when given generated data. That is, the objective of the generator is to generate data that the discriminator classifies as "real". To optimize the performance of the discriminator, minimize the loss of the discriminator when given batches of both real and generated data. That is, the objective of the discriminator is to not be "fooled" by the generator.

Ideally, these strategies result in a generator that generates convincingly realistic data and a discriminator that has learned strong feature representations that are characteristic of the training data. However, [2] argues that the divergences which GANs typically minimize are potentially not continuous with respect to the generator’s parameters, leading to training difficulty and introduces the Wasserstein GAN (WGAN) model that uses the Wasserstein loss to help stabilize training. A WGAN model can still produce poor samples or fail to converge because interactions between the weight constraint and the cost function can result in vanishing or exploding gradients. To address these issues, [3] introduces a gradient penalty which improves stability by penalizing gradients with large norm values at the cost of longer computational time. This type of model is known as a WGAN-GP model.

This example shows how to train a WGAN-GP model that can generate images with similar characteristics to a training set of images.

Load Training Data

Download and extract the Flowers data set [1].

url = "http://download.tensorflow.org/example_images/flower_photos.tgz";
downloadFolder = tempdir;
filename = fullfile(downloadFolder,"flower_dataset.tgz");

imageFolder = fullfile(downloadFolder,"flower_photos");
if ~datasetExists(imageFolder)
    disp("Downloading Flowers data set (218 MB)...")
    websave(filename,url);
    untar(filename,downloadFolder)
end

Create an image datastore containing the photos of the flowers.

datasetFolder = fullfile(imageFolder);

imds = imageDatastore(datasetFolder, ...
    IncludeSubfolders=true);

Augment the data to include random horizontal flipping and resize the images to have size 64-by-64.

augmenter = imageDataAugmenter(RandXReflection=true);
augimds = augmentedImageDatastore([64 64],imds,DataAugmentation=augmenter);

Define Discriminator Network

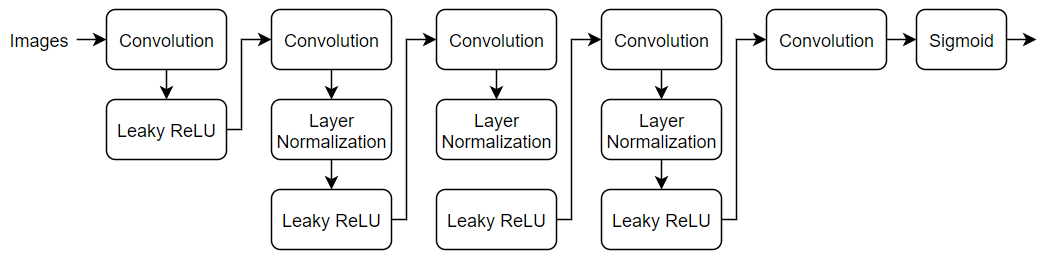
Define the following network, which classifies real and generated 64-by-64 images.

To train the network with a custom training loop and enable automatic differentiation, create a dlnetwork object.

netD = dlnetwork;

Specify layers that take 64-by-64-by-3 images and return a scalar prediction score using a series of convolution layers with batch normalization and leaky ReLU layers and add them to the network. To output the probabilities in the range [0,1], use a sigmoid layer.

• For the convolution layers, specify 5-by-5 filters with an increasing number of filters for each layer. Also specify a stride of 2 and padding of the output.

• For the leaky ReLU layers, specify a scale of 0.2.

• For the final convolution layer, specify one 4-by-4 filter.

numFilters = 64;
scale = 0.2;

inputSize = [64 64 3];
filterSize = 5;

layersD = [
    imageInputLayer(inputSize,Normalization="none")
    convolution2dLayer(filterSize,numFilters,Stride=2,Padding="same")
    leakyReluLayer(scale)
    convolution2dLayer(filterSize,2*numFilters,Stride=2,Padding="same")
    layerNormalizationLayer
    leakyReluLayer(scale)
    convolution2dLayer(filterSize,4*numFilters,Stride=2,Padding="same")
    layerNormalizationLayer
    leakyReluLayer(scale)
    convolution2dLayer(filterSize,8*numFilters,Stride=2,Padding="same")
    layerNormalizationLayer
    leakyReluLayer(scale)
    convolution2dLayer(4,1)
    sigmoidLayer];

netD = addLayers(netD, layersD);

Initialize learnable and state parameters of the network.

netD = initialize(netD);

Define Generator Network

Define the following network architecture, which generates images from 1-by-1-by-100 arrays of random values:

To train the network with a custom training loop and enable automatic differentiation, create a dlnetwork object.

netG = dlnetwork;

This network:

• Converts the random vectors of size 100 to 4-by-4-by-512 arrays using a project and reshape layer.

• Upscales the resulting arrays to 64-by-64-by-3 arrays using a series of transposed convolution layers and ReLU layers.

Define this network architecture as a layer array and add them to the network. Specify the following network properties.

• For the transposed convolution layers, specify 5-by-5 filters with a decreasing number of filters for each layer, a stride of 2, and cropping of the output on each edge.

• For the final transposed convolution layer, specify three 5-by-5 filters corresponding to the three RGB channels of the generated images, and the output size of the previous layer.

• At the end of the network, include a tanh layer.

To project and reshape the noise input, use the custom layer projectAndReshapeLayer, attached to this example as a supporting file. The projectAndReshape layer upscales the input using a fully connected operation and reshapes the output to the specified size.

filterSize = 5;
numFilters = 64;
numLatentInputs = 100;

projectionSize = [4 4 512];

layersG = [
    featureInputLayer(numLatentInputs,Normalization="none")
    projectAndReshapeLayer(projectionSize);
    transposedConv2dLayer(filterSize,4*numFilters)
    reluLayer
    transposedConv2dLayer(filterSize,2*numFilters,Stride=2,Cropping="same")
    reluLayer
    transposedConv2dLayer(filterSize,numFilters,Stride=2,Cropping="same")
    reluLayer
    transposedConv2dLayer(filterSize,3,Stride=2,Cropping="same")
    tanhLayer];

netG = addLayers(netG, layersG);

Initialize learnable and state parameters of the network.

netG = initialize(netG);

Define Model Loss Functions

Create the functions modelLossD and modelLossG listed in the Model Loss Functions section of the example, that calculate the gradients of the discriminator and generator loss with respect to the learnable parameters of the discriminator and generator networks, respectively.

The function modelLossD takes as input the generator and discriminator networks, a mini-batch of input data, an array of random values, and the lambda value used for the gradient penalty, and returns the loss and the gradients of the loss with respect to the learnable parameters in the discriminator.

The function modelLossG takes as input the generator and discriminator networks and an array of random values, and returns the loss and the gradients of the loss with respect to the learnable parameters in the generator.

Specify Training Options

To train a WGAN-GP model, you must train the discriminator for more iterations than the generator. In other words, for each generator iteration, you must train the discriminator for multiple iterations.

Train with a mini-batch size of 64 for 10,000 generator iterations. For larger datasets, you might need to train for more iterations.

miniBatchSize = 64;
numIterationsG = 10000;

For each generator iteration, train the discriminator for 5 iterations.

numIterationsDPerG = 5;

For the WGAN-GP loss, specify a lambda value of 10. The lambda value controls the magnitude of the gradient penalty added to the discriminator loss.

lambda = 10;

Specify the options for Adam optimization:

• For the discriminator network, specify a learning rate of 0.0002.

• For the generator network, specify a learning rate of 0.001.

• For both networks, specify a gradient decay factor of 0 and a squared gradient decay factor of 0.9.

learnRateD = 2e-4;
learnRateG = 1e-3;
gradientDecayFactor = 0;
squaredGradientDecayFactor = 0.9;

Display the generated validation images every 20 generator iterations.

validationFrequency = 20;

Train Model

Use minibatchqueue to process and manage the mini-batches of images. For each mini-batch:

• Use the custom mini-batch preprocessing function preprocessMiniBatch (defined at the end of this example) to rescale the images in the range [-1,1].

• Discard any partial mini-batches.

• Format the image data with the dimension labels "SSCB" (spatial, spatial, channel, batch).

• Train on a GPU if one is available. When the OutputEnvironment option of minibatchqueue is "auto", minibatchqueue converts each output to a gpuArray if a GPU is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox) (Parallel Computing Toolbox).

The minibatchqueue object, by default, converts the data to dlarray objects with underlying type single.

augimds.MiniBatchSize = miniBatchSize;

mbq = minibatchqueue(augimds,...
    MiniBatchSize=miniBatchSize,...
    PartialMiniBatch="discard",...
    MiniBatchFcn=@preprocessMiniBatch,...
    MiniBatchFormat="SSCB");

Train the model using a custom training loop. Loop over the training data and update the network parameters at each iteration. To monitor the training progress, display a batch of generated images using a held-out array of random values to input into the generator as well as a plot of the scores.

Initialize the parameters for Adam.

trailingAvgD = [];
trailingAvgSqD = [];
trailingAvgG = [];
trailingAvgSqG = [];

To monitor training progress, display a batch of generated images using a held-out batch of fixed arrays of random values fed into the generator and plot the network scores.

Create an array of held-out random values.

numValidationImages = 25;
ZValidation = randn(numLatentInputs,numValidationImages,"single");

Convert the data to dlarray objects and specify the dimension labels "SSCB" (spatial, spatial, channel, batch).

ZValidation = dlarray(ZValidation,"CB");

For GPU training, convert the data to gpuArray objects.

if canUseGPU
    ZValidation = gpuArray(ZValidation);
end

Initialize the training progress plots. Create a figure and resize it to have twice the width.

f = figure;
f.Position(3) = 2*f.Position(3);

Create a subplot for the generated images and the network scores.

imageAxes = subplot(1,2,1);
scoreAxes = subplot(1,2,2);

Initialize the animated lines for the loss plot.

C = colororder;
lineLossD = animatedline(scoreAxes,Color=C(1,:));
lineLossDUnregularized = animatedline(scoreAxes,Color=C(2,:));
legend("With Gradient Penalty","Unregularized")
xlabel("Generator Iteration")
ylabel("Discriminator Loss")
grid on

Train the WGAN-GP model by looping over mini-batches of data.

For numIterationsDPerG iterations, train the discriminator only. For each mini-batch:

• Evaluate the discriminator model loss and gradients using dlfeval and the modelLossD function.

• Update the discriminator network parameters using the adamupdate function.

After training the discriminator for numIterationsDPerG iterations, train the generator on a single mini-batch.

• Evaluate the generator model loss and gradients using dlfeval and the modelLossG function.

• Update the generator network parameters using the adamupdate function.

After updating the generator network:

• Plot the losses of the two networks.

• After every validationFrequency generator iterations, display a batch of generated images for a fixed held-out generator input.

After passing through the data set, shuffle the mini-batch queue.

Training can take some time to run and may require many iterations to output good images.

iterationG = 0;
iterationD = 0;
start = tic;

% Loop over mini-batches
while iterationG < numIterationsG
    iterationG = iterationG + 1;

    % Train discriminator only
    for n = 1:numIterationsDPerG
        iterationD = iterationD + 1;

        % Reset and shuffle mini-batch queue when there is no more data.
        if ~hasdata(mbq)
            shuffle(mbq);
        end

        % Read mini-batch of data.
        X = next(mbq);

        % Generate latent inputs for the generator network. Convert to
        % dlarray and specify the dimension labels "CB" (channel, batch).
        Z = randn([numLatentInputs size(X,4)],like=X);
        Z = dlarray(Z,"CB");

        % Evaluate the discriminator model loss and gradients using dlfeval and the
        % modelLossD function listed at the end of the example.
        [lossD, lossDUnregularized, gradientsD] = dlfeval(@modelLossD, netD, netG, X, Z, lambda);

        % Update the discriminator network parameters.
        [netD,trailingAvgD,trailingAvgSqD] = adamupdate(netD, gradientsD, ...
            trailingAvgD, trailingAvgSqD, iterationD, ...
            learnRateD, gradientDecayFactor, squaredGradientDecayFactor);
    end

    % Generate latent inputs for the generator network. Convert to dlarray
    % and specify the dimension labels "CB" (channel, batch).
    Z = randn([numLatentInputs size(X,4)],like=X);
    Z = dlarray(Z,"CB");

    % Evaluate the generator model loss and gradients using dlfeval and the
    % modelLossG function listed at the end of the example.
    [~,gradientsG] = dlfeval(@modelLossG, netG, netD, Z);

    % Update the generator network parameters.
    [netG,trailingAvgG,trailingAvgSqG] = adamupdate(netG, gradientsG, ...
        trailingAvgG, trailingAvgSqG, iterationG, ...
        learnRateG, gradientDecayFactor, squaredGradientDecayFactor);

    % Every validationFrequency generator iterations, display batch of
    % generated images using the held-out generator input
    if mod(iterationG,validationFrequency) == 0 || iterationG == 1
        % Generate images using the held-out generator input.
        XGeneratedValidation = predict(netG,ZValidation);

        % Tile and rescale the images in the range [0 1].
        I = imtile(extractdata(XGeneratedValidation));
        I = rescale(I);

        % Display the images.
        subplot(1,2,1);
        image(imageAxes,I)
        xticklabels([]);
        yticklabels([]);
        title("Generated Images");
    end

    % Update the scores plot
    subplot(1,2,2)

    lossD = double(lossD);
    lossDUnregularized = double(lossDUnregularized);
    addpoints(lineLossD,iterationG,lossD);
    addpoints(lineLossDUnregularized,iterationG,lossDUnregularized);

    D = duration(0,0,toc(start),Format="hh:mm:ss");
    title( ...
        "Iteration: " + iterationG + ", " + ...
        "Elapsed: " + string(D))
    drawnow
end

Here, the discriminator has learned a strong feature representation that identifies real images among generated images. In turn, the generator has learned a similarly strong feature representation that allows it to generate images similar to the training data.

Generate New Images

To generate new images, use the predict function on the generator with a dlarray object containing a batch of random vectors. To display the images together, use the imtile function and rescale the images using the rescale function.

Create a dlarray object containing a batch of 25 random vectors to input to the generator network.

ZNew = randn(numLatentInputs,25,"single");
ZNew = dlarray(ZNew,"CB");

To generate images using the GPU, also convert the data to gpuArray objects.

if canUseGPU
    ZNew = gpuArray(ZNew);
end

Generate new images using the predict function with the generator and the input data.

XGeneratedNew = predict(netG,ZNew);

Display the images.

I = imtile(extractdata(XGeneratedNew));
I = rescale(I);
figure
image(I)
axis off
title("Generated Images")

Model Loss Functions

Discriminator Model Loss Function

The function modelLossD takes as input the generator and discriminator dlnetwork objects netG and netD, a mini-batch of input data X, an array of random values Z, and the lambda value used for the gradient penalty, and returns the loss and the gradients of the loss with respect to the learnable parameters in the discriminator.

Given an image $$X$$, a generated image $$\underset{}{\overset{\sim }{X}}$$, define $$\underset{}{\overset{ˆ}{X}}=ϵX+(1-ϵ)\underset{}{\overset{\sim }{X}}$$ for some random $$ϵ\in U(0,1)$$.

For the WGAN-GP model, given the lambda value $$\lambda$$, the discriminator loss is given by

$${\text{loss}}_D=\underset{}{\overset{\sim }{Y}}-Y+\lambda {({\Vert {\nabla }_{\underset{}{\overset{ˆ}{X}}}\underset{}{\overset{ˆ}{Y}}\Vert }_2-1)}^2,$$

where $$Y$$, $$\underset{}{\overset{\sim }{Y}}$$, and $$\underset{}{\overset{ˆ}{Y}}$$ denote the output of the discriminator for the inputs $$X$$, $$\underset{}{\overset{\sim }{X}}$$, and $$\underset{}{\overset{ˆ}{X}}$$, respectively, and $${\nabla }_{\underset{}{\overset{ˆ}{X}}}\underset{}{\overset{ˆ}{Y}}$$ denotes the gradients of the output $$\underset{}{\overset{ˆ}{Y}}$$ with respect to $$\underset{}{\overset{ˆ}{X}}$$. For a mini-batch of data, use a different value of $$ϵ$$ for each observation and calculate the mean loss.

The gradient penalty $$\lambda {({\Vert {\nabla }_{\underset{}{\overset{ˆ}{X}}}\underset{}{\overset{ˆ}{Y}}\Vert }_2-1)}^2$$ improves stability by penalizing gradients with large norm values. The lambda value controls the magnitude of the gradient penalty added to the discriminator loss.

function [lossD, lossDUnregularized, gradientsD] = modelLossD(netD, netG, X, Z, lambda)

% Calculate the predictions for real data with the discriminator network.
YPred = forward(netD, X);

% Calculate the predictions for generated data with the discriminator
% network.
XGenerated = forward(netG,Z);
YPredGenerated = forward(netD, XGenerated);

% Calculate the loss.
lossDUnregularized = mean(YPredGenerated - YPred);

% Calculate and add the gradient penalty. 
epsilon = rand([1 1 1 size(X,4)],like=X);
XHat = epsilon.*X + (1-epsilon).*XGenerated;
YHat = forward(netD, XHat);

% Calculate gradients. To enable computing higher-order derivatives, set
% EnableHigherDerivatives to true.
gradientsHat = dlgradient(sum(YHat),XHat,EnableHigherDerivatives=true);
gradientsHatNorm = sqrt(sum(gradientsHat.^2,1:3) + 1e-10);
gradientPenalty = lambda.*mean((gradientsHatNorm - 1).^2);

% Penalize loss.
lossD = lossDUnregularized + gradientPenalty;

% Calculate the gradients of the penalized loss with respect to the
% learnable parameters.
gradientsD = dlgradient(lossD, netD.Learnables);

end

Generator Model Loss Function

The function modelLossG takes as input the generator and discriminator dlnetwork objects netG and netD, and an array of random values Z, and returns the loss and the gradients of the loss with respect to the learnable parameters in the generator.

Given a generated image $$\underset{}{\overset{\sim }{X}}$$, the loss for the generator network is given by

$${\text{loss}}_G=-\underset{}{\overset{\sim }{Y}},$$

where $$\underset{}{\overset{\sim }{Y}}$$ denotes the output of the discriminator for the generated image $$\underset{}{\overset{\sim }{X}}$$. For a mini-batch of generated images, calculate the mean loss.

function [lossG,gradientsG] =  modelLossG(netG, netD, Z)

% Calculate the predictions for generated data with the discriminator
% network.
XGenerated = forward(netG,Z);
YPredGenerated = forward(netD, XGenerated);

% Calculate the loss.
lossG = -mean(YPredGenerated);

% Calculate the gradients of the loss with respect to the learnable
% parameters.
gradientsG = dlgradient(lossG, netG.Learnables);

end

Mini-Batch Preprocessing Function

The preprocessMiniBatch function preprocesses the data using the following steps:

1. Extract the image data from the input cell array and concatenate into a numeric array.

2. Rescale the images to be in the range [-1,1].

function X = preprocessMiniBatch(data)

% Concatenate mini-batch
X = cat(4,data{:});

% Rescale the images in the range [-1 1].
X = rescale(X,-1,1,InputMin=0,InputMax=255);

end

References

1. The TensorFlow Team. Flowers http://download.tensorflow.org/example_images/flower_photos.tgz

2. Arjovsky, Martin, Soumith Chintala, and Léon Bottou. "Wasserstein GAN." arXiv preprint arXiv:1701.07875 (2017).

3. Gulrajani, Ishaan, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron C. Courville. "Improved training of Wasserstein GANs." In Advances in neural information processing systems, pp. 5767-5777. 2017.