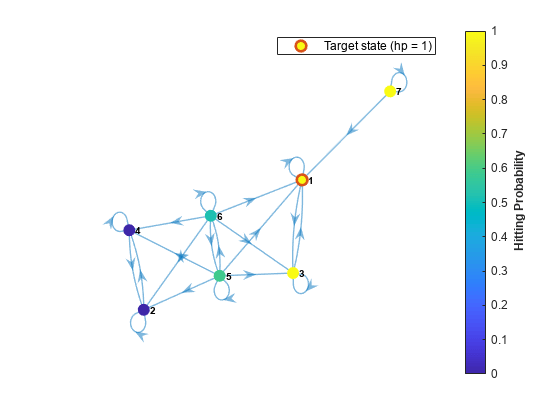
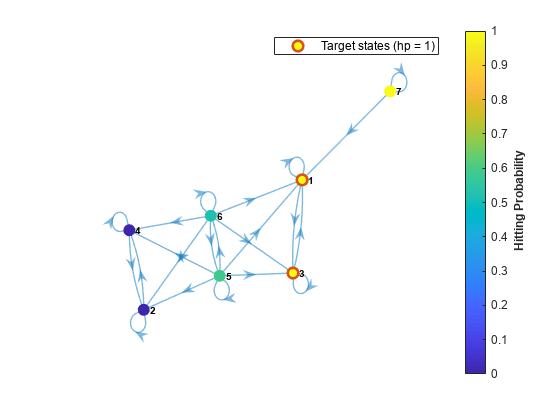
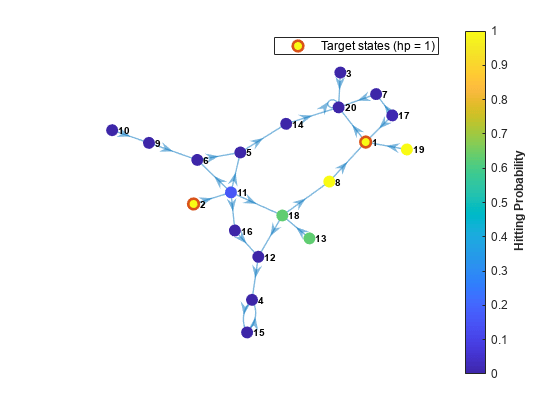
hitprob
Compute Markov chain hitting probabilities
Syntax
Description
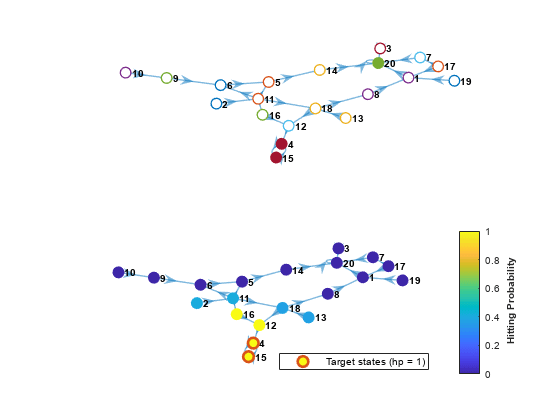
Examples
Input Arguments
Output Arguments
More About
References
[1] Norris, J. R. Markov Chains. Cambridge, UK: Cambridge University Press, 1997.
Version History
Introduced in R2019b