Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

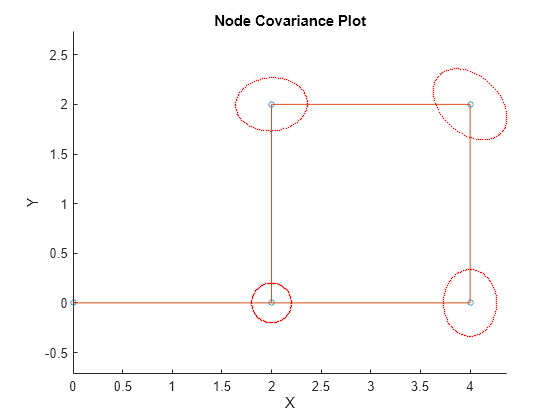
nodeCovariance

Obtener la covarianza de estado de los nodos en el gráfico factorial

Desde R2024b

Sintaxis

covariance = nodeCovariance(fg,nodeIDs)

Descripción

covariance = nodeCovariance(fg,nodeIDs) obtiene las covarianzas almacenadas de los nodos con los ID de nodo especificados en el gráfico de factores especificado. Debe optimizar el gráfico de factores utilizando la función optimize con la estimación de covarianza habilitada antes de poder recuperar las covarianzas de los nodos almacenados. Para obtener más información sobre el algoritmo de estimación de covarianza y cómo habilitar la estimación de covarianza, consulte el objeto optimize y factorGraphSolverOptions, respectivamente.

Ejemplos

Obtener la covarianza del estado del nodo a partir del gráfico de factores

Crea un gráfico factorial con 5 nodos de pose. Para que sea más fácil ver el cambio en la covarianza del estado del nodo en este ejemplo, especifique la misma matriz de información para todos los factores.

fg = factorGraph;
f1 = factorTwoPoseSE2([1 2],Measurement=[2 0 0],Information=[25 0 0; 0 25 0; 0 0 100]);
f2 = factorTwoPoseSE2([2 3],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
f3 = factorTwoPoseSE2([3 4],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
f4 = factorTwoPoseSE2([4 5],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
addFactor(fg,f1);
addFactor(fg,f2);
addFactor(fg,f3);
addFactor(fg,f4);

Añade un cierre de bucle entre el segundo y el quinto nodo usando un factor.

f5 = factorTwoPoseSE2([5 2],Measurement=[2 0 pi/2],Information=[25 0 0; 0 25 0; 0 0 100]);
addFactor(fg,f5);

Repara el primer nodo e inicializa los estados del nodo. El primer estado puede permanecer en el valor predeterminado.

fixNode(fg,1)
nodeState(fg,2:5,[2 0 0; 4 0 pi/2; 4 2 pi; 2 2 3*pi/2]);

Visualice el gráfico de factores.

show(fg);
title("Factor Graph with Loop Closure Before Optimization")
axis equal
xlabel("X")
ylabel("Y")
hold on

Cree opciones de solucionador de gráficos factoriales que indiquen al solucionador que debe estimar la covarianza del estado del nodo para todos los tipos de nodos en el gráfico factorial.

opts = factorGraphSolverOptions(StateCovarianceType="all-types");

Optimice el gráfico con las opciones personalizadas para estimar y almacenar la covarianza del estado del nodo.

optimize(fg,opts);

Obtenga los identificadores de los nodos de pose SE(2) y obtenga sus matrices de covarianza de estado.

se2nodes = nodeIDs(fg,NodeType="POSE_SE2");
se2Cov = nodeCovariance(fg,se2nodes);

Extraer los elementos diagonales de las matrices de covarianza de estados. Tenga en cuenta que los valores de covarianza de estado del primer nodo son cero porque ese nodo es fijo.

se2Cov2Diag = [diag(se2Cov(:,:,1))';
               diag(se2Cov(:,:,2))';
               diag(se2Cov(:,:,3))';
               diag(se2Cov(:,:,4))';
               diag(se2Cov(:,:,5))']

se2Cov2Diag = 5×3

         0         0         0
    0.0400    0.0400    0.0100
    0.0720    0.1120    0.0165
    0.1380    0.1280    0.0180
    0.1300    0.0720    0.0165

Grafique las covarianzas del estado del nodo. Tenga en cuenta que la covarianza graficada aumenta debido a la acumulación de deriva con cada nodo consecutivo hasta el nodo 5, que tiene una covarianza menor debido a la información de estado adicional proporcionada por el cierre del bucle.

states = nodeState(fg,se2nodes);
exampleHelperPlot2DCovariance(se2Cov,states);
title("Node Covariance Plot")
axis equal

Argumentos de entrada

fg — Gráfico de factores

objeto factorGraph

Gráfico factorial, especificado como un objeto factorGraph.

nodeIDs — Identificadores de nodos para los cuales recuperar covarianzas de estado

N- vector fila de elementos enteros no negativos

Identificadores de nodos para los cuales recuperar covarianzas de estado, especificados como un vector fila de elementos N de números enteros no negativos. N es el número de identificadores de nodos especificados.

Todos los ID de nodo deben especificar nodos del mismo tipo. Y para obtener la covarianza del estado del nodo para cualquier nodo, primero debe optimizar el gráfico de factores con opciones de solucionador personalizadas que especifiquen para qué tipo de nodo estimar y almacenar la covarianza del estado. Para especificar el tipo de nodo a utilizar, establezca la propiedad StateCovarianceType del objeto factorGraphSolverOptions en uno o más tipos de nodo deseados.

Argumentos de salida

covariance — Covarianzas del estado del nodo

Matriz M-por-M-por-N

Covarianzas del estado del nodo, devueltas como una matriz M por M por N. Cada página de la matriz representa la matriz de covarianza de estados de un nodo. N es el número de identificaciones de nodos especificados.

El tamaño de las matrices de covarianza depende del tipo de nodo de los ID de nodo especificados:

• "POSE_SE2" — Matriz de 3 por 3

• "POSE_SE3" — Matriz de 7 por 7

• "POINT_XY" — Matriz de 2 por 2

• "POINT_XYZ" — Matriz de 3 por 3

• "IMU_BIAS" — Matriz de 6 x 6

• "VEL3" — Matriz de 3 por 3

Nota

Para obtener la covarianza del estado del nodo para un tipo de nodo, primero debe optimizar el gráfico de factores con opciones de solucionador personalizadas que especifiquen el tipo de nodo para el cual estimar y almacenar la covarianza del estado. Para especificar el tipo de nodo a utilizar, establezca la propiedad StateCovarianceType del objeto factorGraphSolverOptions en uno o más tipos de nodo deseados.

Capacidades ampliadas

Generación de código C/C++

Genere código C y C++ mediante MATLAB® Coder™.

Al generar código C portable con un compilador C++, debe especificar el empaquetado jerárquico con encabezados no mínimos. Para obtener más información sobre las opciones de embalaje, consulte la función packNGo (MATLAB Coder).

Historial de versiones

Introducido en R2024b

Consulte también

factorGraph | factorGraphSolverOptions | optimize | nodeIDs