rottraj
Generate trajectories between orientation rotation matrices
Syntax
Description
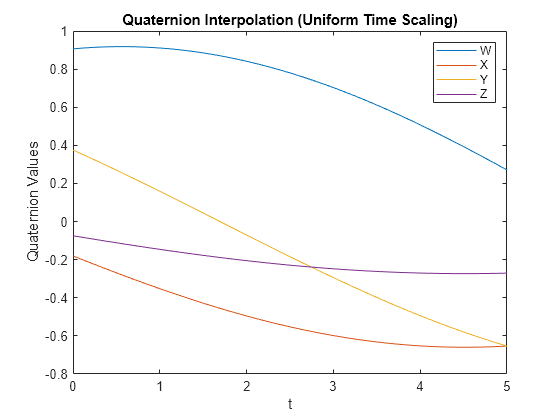
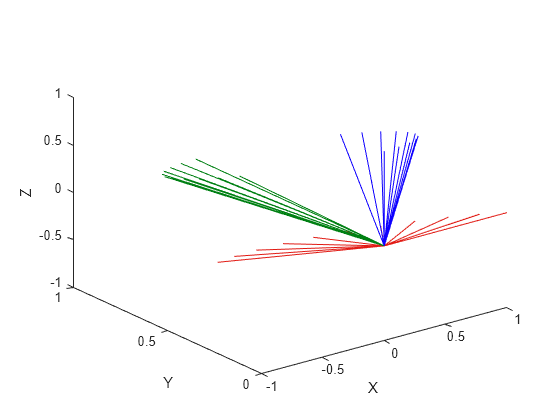
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
When specifying your
r0andrFinput arguments as a 3-by-3 rotation matrix, they are converted to aquaternionobject before interpolating the trajectory. If your rotation matrix does not follow a right-handed coordinate system or does not have a direct conversion to quaternions, this conversion may result in different initial and final rotations in the output trajectory.
References
[1] Dam, Erik B., Martin Koch, and Martin Lillholm. Quaternions, Interpolation and Animation. Technical Report DIKU-TR-98/5 (July 1998). http://web.mit.edu/2.998/www/QuaternionReport1.pdf
[2] Graf, Basile. Quaternions and Dynamics. arXiv:0811.2889 [math.DS] (2008). https://arxiv.org/pdf/0811.2889.pdf
[3] Lynch, Kevin M., and Frank C. Park. Modern Robotics: Mechanics, Planning, and Control. Cambridge University Press, 2017.
Extended Capabilities
Version History
Introduced in R2019aSee Also
bsplinepolytraj | contopptraj | cubicpolytraj | quinticpolytraj | transformtraj | trapveltraj | quaternion