La función de Dirichlet

La función diric calcula la función de Dirichlet, a veces denominada función sinc periódica o sinc con alias, para un vector o matriz de entrada x. La función de Dirichlet viene definida por

$\begin{array}{l}D(x)=\text{cases}{\displaystyle \frac{\sin (Nx/2)}{{\displaystyle N\sin (x/2)}}},\\ \text{\&}x\ne 2\pi k\text{,}\end{array}$

donde $$N$$ es un entero positivo especificado por el usuario. Si $$N$$ es impar, la función de Dirichlet tiene un periodo de $$2\pi$$; si $$N$$ es par, su periodo es $$4\pi$$. La magnitud de esta función es $$1/N$$ veces la magnitud de la transformada de Fourier en tiempo discreto de la ventana rectangular de $$N$$ puntos.

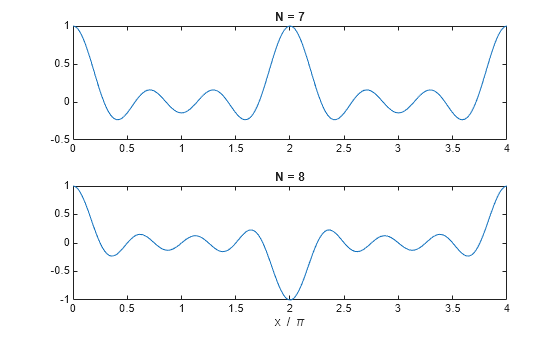
Para representar la función de Dirichlet entre 0 y $$4\pi$$ para $$N=7$$ y $$N=8$$, utilice

x = linspace(0,4*pi,300);

subplot(2,1,1)
plot(x/pi,diric(x,7))
title('N = 7')

subplot(2,1,2)
plot(x/pi,diric(x,8))
title('N = 8')
xlabel('x / \pi')

Consulte también

diric | sinc