diric
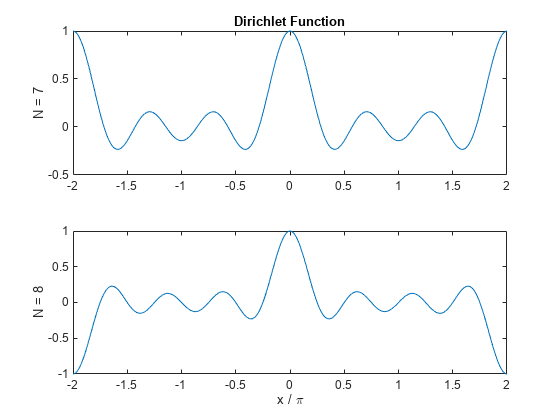
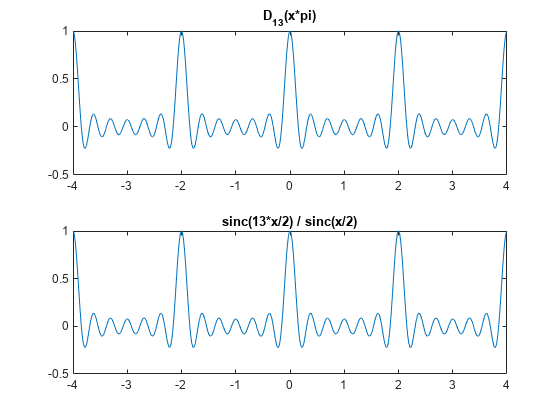
Función de Dirichlet o sinc periódica
Sintaxis
Descripción
y = diric(x,n)n evaluada en los elementos del arreglo de entrada x.
Ejemplos
Argumentos de entrada
Argumentos de salida
Más acerca de
Capacidades ampliadas
Historial de versiones
Introducido antes de R2006a