Designing Motor Control Algorithms for Optimum Performance and Efficient Operation of an Electric Two-Wheeler
Overview
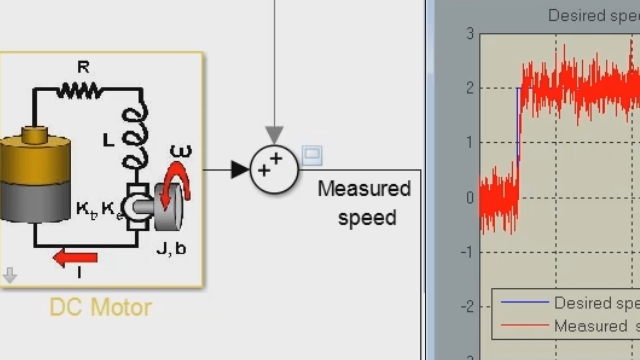
With the advent of electrification in the 2-W industry, motor simulation and motor control design have grown significantly. Speed, torque, and other performance characteristics are regulated by motor control algorithms. The focus of this session is on latest capabilities that are unique to the development and application of motor control algorithms wherein you will discover an effective process for:
- Motor control workflows for BLDC, PMSM, IM as well as some emerging motor types such as SRM
- Designing and tuning control algorithms such as FOC, FWC, and MPC
- Generating ANSI, ISO, or processor-optimized C code and HDL code for real-time testing and implementation
- Verifying and testing control algorithms using simulation and prototyping hardware
About the Presenters
Rahul Choudhary, Senior Application Engineer, MathWorks
Rahul is a Senior Application Engineer at MathWorks India and specializes in the field of System Modeling and Control Design. He has over 9 years of experience in power electronics control, motor control, multi-domain modeling, and real-time simulation. Before joining MathWorks, Rahul worked with Eaton India Engineering Centre as a Control Engineer where he was involved in developing prognostics and health monitoring algorithms for proof-of-concept projects for their electrical business using MATLAB and Simulink. He holds a master’s degree in Systems and Control Engineering from Indian Institute of Technology Bombay, Mumbai and a bachelor’s degree in Electronics and Instrumentation Engineering from Institute of Engineering and Technology, Lucknow, India.
Ananth Kumar Selvaraj, Senior Tech Lead, MathWorks
Ananth Kumar Selvaraj is a Senior Tech Lead at MathWorks India, specialized in Power electronics and Motor control. He and his team members work on Model Based Design workflows and tools for developing motor control solutions. Ananth Kumar brings 19 years of experience in Embedded and Control design from Industrial and Automation domain. Prior to joining MathWorks, Ananth Kumar worked for National Instruments, Schneider Electric and KONE Elevators as an expert in embedded and control engineering for Power electronics and Motion control. He holds a bachelor’s degree in electrical and electronics engineering and master’s degree in Mechatronics engineering.
Recorded: 22 Sep 2022