tf

Modelo de función de transferencia

Descripción

Use tf para crear modelos de función de transferencia de valores reales o complejos, o bien para convertir modelos de sistemas dinámicos a la forma de función de transferencia.

Una función de transferencia es una representación en el dominio de la frecuencia de un sistema lineal invariante en el tiempo. Por ejemplo, considere un sistema dinámico SISO en tiempo continuo representado por la función de transferencia sys(s) = N(s)/D(s), donde s = jw, y N(s) y D(s) de denominan numerador y denominador polinomiales, respectivamente. El objeto de modelo tf puede representar funciones de transferencia SISO o MIMO en tiempo continuo o tiempo discreto.

Para crear un objeto de modelo de función de transferencia, puede especificar sus coeficientes directamente o convertir un modelo de otro tipo (por ejemplo, un modelo de espacio de estados ss) a la forma de función de transferencia. Para más información, consulte Funciones de transferencia.

También puede usar tf para crear modelos generalizados en espacio de estados (genss) o modelos de espacio de estados con incertidumbre (uss (Robust Control Toolbox)).

Creación

Sintaxis

sys = tf(numerator,denominator)

sys = tf(numerator,denominator,ts)

sys = tf(numerator,denominator,ltiSys)

sys = tf(m)

sys = tf(___,PropertyName=Value)

sys = tf(ltiSys)

sys = tf(ltiSys,Name=Value)

sys = tf(ltiSys,component)

s = tf('s')

z = tf('z',ts)

Descripción

Crear un modelo de función de transferencia

sys = tf(numerator,denominator) crea un modelo de función de transferencia en tiempo continuo mediante la asignación de las propiedades Numerator y Denominator. Por ejemplo, considere un sistema dinámico SISO en tiempo continuo representado por la función de transferencia sys(s) = N(s)/D(s). En este caso, los argumentos de entrada numerator y denominator serán los coeficientes de N(s) y D(s), respectivamente.

sys = tf(numerator,denominator,ts) crea un modelo de función de transferencia en tiempo discreto mediante la asignación de las propiedades Numerator, Denominator y Ts. Por ejemplo, considere un sistema dinámico SISO en tiempo discreto representado por la función de transferencia sys(z) = N(z)/D(z). En este caso, los argumentos de entrada numerator y denominator serán los coeficientes de N(z) y D(z), respectivamente. Si no desea especificar el tiempo de muestreo, el argumento de entrada ts se debe establecer en -1.

sys = tf(numerator,denominator,ltiSys) crea un modelo de función de transferencia cuyas propiedades, incluido el tiempo de muestreo, se heredan del modelo de sistema dinámico ltiSys.

sys = tf(m) crea un modelo de función de transferencia que representa la ganancia estática m.

sys = tf(___,PropertyName=Value) establece las propiedades del modelo de función de transferencia usando uno o más argumentos de par nombre-valor para cualquiera de las combinaciones de entrada/argumento anteriores.

Convertir a un modelo de función de transferencia

sys = tf(ltiSys) convierte el modelo de sistema dinámico ltiSys en un modelo de función de transferencia.

sys = tf(ltiSys,Name=Value) obtiene una representación de una función de transferencia truncada del modelo disperso ltiSys calculando ceros y polos en base a uno o más de los argumentos nombre-valor especificados. Dado que este método calcula ceros para cada par entrada-salida, es más adecuado para modelos con tamaños pequeños de entrada-salida. (desde R2025a)

sys = tf(ltiSys,component) convierte el componente component especificado de ltiSys a la forma de función de transferencia. Use esta sintaxis solo si ltiSys es un modelo identificado lineal invariante en el tiempo (LTI).

Crear variable para expresión racional

s = tf('s') crea una variable especial s que puede usar en una expresión racional para crear un modelo de función de transferencia en tiempo continuo. A veces, usar una expresión racional es más fácil e intuitivo que especificar los coeficientes polinomiales.

z = tf('z',ts) crea una variable especial z que puede usar en una expresión racional para crear un modelo de función de transferencia en tiempo discreto. Si no desea especificar el tiempo de muestreo, el argumento de entrada ts se debe establecer en -1.

Argumentos de entrada

numerator — Coeficientes del numerador de la función de transferencia

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Coeficientes del numerador de la función de transferencia, especificados como:

• Un vector fila de coeficientes polinomiales.

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar una función de transferencia MIMO, donde Ny es el número de salidas y Nu es el número de entradas.

Cuando cree la función de transferencia, los coeficientes del numerador se deben especificar en orden decreciente de potencias. Por ejemplo, si el numerador de la función de transferencia es 3s^2-4s+5, especifique [3 -4 5] como numerator. Si se trata de una función de transferencia en tiempo discreto con el numerador 2z-1, especifique [2 -1] como numerator.

También es una propiedad del objeto tf. Para más información, consulte Numerator.

denominator — Coeficientes del denominador de la función de transferencia

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Coeficientes del denominador, especificados como:

• Un vector fila de coeficientes polinomiales.

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar una función de transferencia MIMO, donde Ny es el número de salidas y Nu es el número de entradas.

Cuando cree la función de transferencia, los coeficientes del denominador se deben especificar en orden decreciente de potencias. Por ejemplo, si el denominador de la función de transferencia es 7s^2+8s-9, especifique [7 8 -9] como denominator. Si se trata de una función de transferencia en tiempo discreto con el denominador 2z^2+1, especifique [2 0 1] como denominator.

También es una propiedad del objeto tf. Para más información, consulte Denominator.

ts — Tiempo de muestreo

escalar

Tiempo de muestreo, especificado como un escalar. También es una propiedad del objeto tf. Para más información, consulte Ts.

ltiSys — Sistema dinámico

modelo de sistema dinámico | arreglo de modelos

Sistema dinámico, especificado como un modelo de sistema dinámico SISO o MIMO, o bien un arreglo de modelos de sistemas dinámicos. Se admiten los siguientes tipos de sistemas dinámicos:

• Modelos LTI numéricos en tiempo continuo o en tiempo discreto, como modelos tf, zpk, ss o pid.

  Si ltiSys es un modelo de espacio de estados disperso (sparss o mechss), el software calcula la aproximación de una función de transferencia truncada calculando polos y ceros en una banda de frecuencia de enfoque especificada. Para modelos dispersos, utilice los argumentos nombre-valor para especificar opciones de cálculo. Si no especifica ninguna opción, el software calcula hasta los 1000 primeros polos y ceros con la magnitud más pequeña. Además, obtener esta aproximación solo es aplicable a modelos con una representación de sparss válida. (desde R2025a)

• Modelos LTI generalizados o con incertidumbre, como modelos genss o uss (Robust Control Toolbox). El uso de modelos con incertidumbre requiere Robust Control Toolbox™.

  En este caso, la función de transferencia resultante asume

  • valores actuales de los componentes ajustables para los bloques de diseño de control ajustables.

  • valores nominales del modelo para los bloques de diseño de control con incertidumbre.

• Modelos LTI identificados, como modelos idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox) y idgrey (System Identification Toolbox). Para seleccionar el componente del modelo identificado que desea convertir, especifique component. Si no especifica component, el comportamiento predeterminado de tf es convertir el componente medido del modelo identificado. El uso de modelos identificados requiere System Identification Toolbox™.

m — Ganancia estática

escalar | matriz

Ganancia estática, especificada como un escalar o una matriz. La ganancia estática o ganancia de estado estacionario de un sistema representa la relación entre la salida y la entrada en estado estacionario.

component — Componente del modelo identificado

'measured' (predeterminado) | 'noise' | 'augmented'

Componente del modelo identificado que se desea convertir, especificado con una de las siguientes opciones:

• 'measured': convierte el componente medido de sys.

• 'noise': convierte el componente de ruido de sys

• 'augmented': convierte tanto el componente medido como el componente de ruido de sys.

component solo es válido cuando sys es un modelo LTI identificado.

Para más información acerca de los modelos LTI identificados y sus componentes medidos y de ruido, consulte Identified LTI Models.

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos nombre-valor deben aparecer después de los otros argumentos, aunque el orden de los pares no es importante.

Ejemplo: sys = tf(sparseSys,Focus=[0 100],Display="off")

UseParallel — Utilice cálculo paralelo

0 o false (predeterminado) | 1 o true

Desde R2025a

Utilice el cálculo paralelo durante el cálculo de polos y ceros, especificado como un 0 numérico o lógico (false) o 1 (true).

Cuando UseParallel se establece en true, se puede elegir de manera explícita escalar al entorno paralelo preferido. Habilitar cálculo paralelo puede mejorar el rendimiento durante el cálculo de ceros y polos. Sin embargo, incluso con UseParallel establecida en false, el algoritmo puede utilizar el multiproceso integrado para usar los recursos locales de la mejor manera posible. Para obtener más información, consulte MATLAB Multicore.

Esta opción requiere una licencia de Parallel Computing Toolbox™.

RollOff — Pendiente de atenuación

0 (predeterminado) | escalar no positivo | matriz

Desde R2025a

Pendiente de atenuación, especificada como una matriz o un escalar no positivo.

• Utilice un valor escalar para modelos SISO o cuando la pendiente es uniforme para todos los pares entrada-salida para modelos MIMO.

• Utilice una matriz cuando la pendiente es diferente para cada par entrada-salida para modelos MIMO.

Esta opción permite especificar explícitamente cómo debe atenuar la aproximación más allá del rango de frecuencia especificado. Por ejemplo, Slope de -2 garantiza que la ganancia se desplace a una tasa de al menos –40 dB/década (la tasa de atenuación de 1/s²) más allá de fmax.

Focus — Rango de frecuencia de interés

[0 Inf] (predeterminado) | vector

Desde R2025a

Rango de frecuencia de interés, especificado como vector con la forma [0,fmax]. Cuando se especifica un rango de frecuencia de enfoque, el software calcula solo los polos con frecuencia natural en este rango. En el caso de modelos en tiempo discreto, el software aproxima la frecuencia natural equivalente a través de la transformada de Tustin.

Dado que tf calcula todos los polos y ceros en el rango de frecuencia especificado, normalmente se especifica un rango de frecuencia baja para limitar el cálculo de un gran número de polos y ceros. De forma predeterminada, el enfoque no está especificado ([0 Inf]) y el algoritmo calcula hasta MaxNumber polos y ceros.

MaxNumber — Número máximo de polos y ceros que se desea calcular

1000 (predeterminado) | entero positivo

Desde R2025a

Número máximo de polos y ceros que se desea calcular, especificado como entero positivo. Este valor limita el número de polos y ceros calculados por el algoritmo y el orden de la aproximación del modelo disperso original.

Shift — Desplazamiento espectral

0 (predeterminado) | escalar finito

Desde R2025a

Desplazamiento espectral, especificado como escalar finito.

El software calcula polos con la frecuencia natural en el rango especificado [0,fmax] utilizando iteraciones de potencia inversa para A-sigma*E, que obtiene valores propios más cercanos al desplazamiento sigma. Cuando A es singular y sigma es cero, el algoritmo falla ya que no existe inversa. Por lo tanto, para los modelos dispersos con acción integral (s = 0 o en z = 1 para modelos en tiempo discreto), puede utilizar esta opción para desplazar de manera implícita polos o ceros hacia el valor más cercano a este valor de desplazamiento. Especifique un valor de desplazamiento que no sea igual al valor de un polo o cero existente del modelo original.

Tolerance — Precisión de polos y ceros calculados

1e-12 (predeterminado) | escalar finito positivo

Desde R2025a

Tolerancia para la precisión de polos y ceros calculados, especificada como escalar finito positivo. Este valor controla la convergencia de los valores propios calculados en iteraciones de potencia inversa.

Display — Mostrar u ocultar informe de progreso

"on" (predeterminado) | "off"

Desde R2025a

Mostrar u ocultar informe de progreso, especificado como "off" u "on".

Argumentos de salida

sys — Modelo de sistema de salida

Objeto de modelo tf | Objeto de modelo genss | Objeto de modelo uss

Modelo de sistema de salida, en uno de los siguientes formatos:

• Un objeto de modelo de función de transferencia (tf), si los argumentos de entrada numerator y denominator son arreglos numéricos. sys siempre es un objeto de modelo tf cuando se convierte ltiSys al tipo de modelo tf.

• Un objeto de modelo de espacio de estados generalizado (genss), si los argumentos de entrada numerator o denominator incluyen parámetros ajustables, como parámetros realp o matrices generalizadas (genmat). Para ver un ejemplo, consulte Filtro paso bajo ajustable.

• Un objeto de modelo de espacio de estados con incertidumbre (uss), si los argumentos de entrada numerator o denominator incluyen parámetros con incertidumbre. El uso de modelos con incertidumbre requiere Robust Control Toolbox. Para ver un ejemplo, consulte Transfer Function with Uncertain Coefficients (Robust Control Toolbox).

Propiedades

Numerator — Coeficientes del numerador

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Coeficientes del numerador, especificados como:

• Un vector fila de los coeficientes polinomiales en orden de potencias decrecientes (si el valor de Variable es 's', 'z', 'p' o 'q') o en orden de potencias crecientes (si el valor de Variable es 'z^-1' o 'q^-1').

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar una función de transferencia MIMO, donde Ny es el número de salidas y Nu es el número de entradas. Cada elemento del arreglo de celdas especifica los coeficientes del numerador correspondientes a un par entrada-salida dado. Si especifica tanto Numerator como Denominator como arreglos de celdas, deberán tener las mismas dimensiones.

Los coeficientes de Numerator pueden ser de valores reales o de valores complejos.

Denominator — Coeficientes del denominador

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Coeficientes del denominador, especificados como:

• Un vector fila de los coeficientes polinomiales en orden de potencias decrecientes (si el valor de Variable es 's', 'z', 'p' o 'q') o en orden de potencias crecientes (si el valor de Variable es 'z^-1' o 'q^-1').

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar una función de transferencia MIMO, donde Ny es el número de salidas y Nu es el número de entradas. Cada elemento del arreglo de celdas especifica los coeficientes del numerador correspondientes a un par entrada-salida dado. Si especifica tanto Numerator como Denominator como arreglos de celdas, deberán tener las mismas dimensiones.

Si todas las entradas SISO de una función de transferencia MIMO tienen el mismo denominador, puede especificar Denominator como el vector fila y especificar Numerator como un arreglo de celdas.

Los coeficientes de Denominator pueden ser de valores reales o de valores complejos.

Variable — Variable para la visualización de la función de transferencia

's' (predeterminado) | 'z' | 'p' | 'q' | 'z^-1' | 'q^-1'

Variable de visualización de la función de transferencia, especificada como una de las siguientes opciones:

• 's': la opción predeterminada para modelos en tiempo continuo

• 'z': la opción predeterminada para modelos en tiempo discreto

• 'p': equivalente a 's'

• 'q': equivalente a 'z'

• 'z^-1': la inversa de 'z'

• 'q^-1': equivalente a 'z^-1'

El valor de Variable se muestra en la visualización y, en el caso de los modelos en tiempo discreto, afecta a la interpretación de los vectores de coeficientes de Numerator y Denominator.

• Si el valor de Variable es 's', 'z', 'p' o 'q', los coeficientes se ordenan en potencias decrecientes de la variable. Por ejemplo, considere el vector fila [ak ... a1 a0]. El orden de los polinomios se especifica como $$a_k{z}^k+\mathrm{...}+a_{1}z+a_0$$.

• Si el valor de Variable es 'z^-1' o 'q^-1', los coeficientes se ordenan en potencias crecientes de la variable. Por ejemplo, considere el vector fila [b0 b1 ... bk]. El orden de los polinomios se especifica como $$b_0+b_1{z}^{-1}+\mathrm{...}+b_k{z}^{-k}$$.

Para ver más ejemplos, consulte Especificación del orden de los polinomios en una función de transferencia en tiempo discreto, Modelo de función de transferencia a partir de expresión racional y Modelo de función de transferencia en tiempo discreto a partir de expresión racional.

IODelay — Retardo de transporte

0 (predeterminado) | escalar | Arreglo de Ny por Nu

Retardo de transporte, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de transporte de un sistema SISO, o bien un retardo de transporte común a todos los pares entrada-salida de un sistema MIMO.

• Arreglo de Ny por Nu: especifica retardos de transporte independientes para cada par entrada-salida de un sistema MIMO. Aquí, Ny es el número de salidas y Nu es el número de entradas.

Si se trata de un sistema en tiempo continuo, los retardos de transporte se deben especificar en las unidades dadas por la propiedad TimeUnit. Si se trata de un sistema en tiempo discreto, los retardos de transporte se deben especificar como múltiplos enteros del tiempo de muestreo, Ts.

InputDelay — Retardo de entrada

0 (predeterminado) | escalar | Vector de Nu por 1

Retardo de entrada para cada canal de entrada, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de entrada de un sistema SISO, o bien un retardo común a todas las entradas de un sistema con varias entradas.

• Vector de Nu por 1: especifica retardos de entrada independientes para cada entrada de un sistema con varias entradas, donde Nu es el número de entradas.

Si se trata de un sistema en tiempo continuo, los retardos de entrada se deben especificar en las unidades dadas por la propiedad TimeUnit. Si se trata de un sistema en tiempo discreto, los retardos de entrada se deben especificar como múltiplos enteros del tiempo de muestreo, Ts.

Para más información, consulte Retardos de tiempo en sistemas lineales.

OutputDelay — Retardo de salida

0 (predeterminado) | escalar | Vector de Ny por 1

Retardo de salida para cada canal de salida, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de salida de un sistema SISO, o bien un retardo común a todas las salidas de un sistema con varias salidas.

• Vector de Ny por 1: especifica retardos de salida independientes para cada salida de un sistema con varias salidas, donde Ny es el número de salidas.

Si se trata de un sistema en tiempo continuo, los retardos de salida se deben especificar en las unidades de tiempo dadas por la propiedad TimeUnit. Si se trata de un sistema en tiempo discreto, los retardos de salida se deben especificar como múltiplos enteros del tiempo de muestreo, Ts.

Para más información, consulte Retardos de tiempo en sistemas lineales.

Ts — Tiempo de muestreo

0 (predeterminado) | escalar positivo | -1

Tiempo de muestreo, especificado como:

• 0 si se trata de un sistema en tiempo continuo.

• Un escalar positivo que representa el periodo de muestreo de un sistema en tiempo discreto. Ts se debe especificar en las unidades de tiempo dadas por la propiedad TimeUnit.

• -1 si se trata de un sistema en tiempo discreto con un tiempo de muestreo indefinido.

Nota

Cambiar Ts no discretiza ni remuestrea el modelo. Para la conversión entre representaciones en tiempo continuo y en tiempo discreto, use c2d y d2c. Para cambiar el tiempo de muestreo de un sistema en tiempo discreto use d2d.

TimeUnit — Unidades de la variable tiempo

'seconds' (predeterminado) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

Unidades de la variable tiempo, especificadas como una de las siguientes opciones:

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

Cambiar TimeUnit no afecta a otras propiedades, pero sí cambia el comportamiento general del sistema. Use chgTimeUnit para la conversión entre distintas unidades de tiempo sin modificar el comportamiento del sistema.

InputName — Nombres de los canales de entrada

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Nombres de los canales de entrada, especificados como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una sola entrada.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias entradas.

• '', para no especificar un nombre, para cualquier canal de entrada.

Como alternativa, se pueden asignar nombres a las entradas de un modelo de varias entradas mediante la expansión automática de vectores. Por ejemplo, si sys es un modelo de dos entradas, se puede introducir lo siguiente:

sys.InputName = 'controls';

En este caso, el valor se expandirá automáticamente y los nombres de las entradas serán {'controls(1)';'controls(2)'}.

Se puede usar la notación abreviada u para hacer referencia a la propiedad InputName. Por ejemplo, sys.u es equivalente a sys.InputName.

Utilice InputName para:

• Identificar los canales en la visualización y las gráficas del modelo.

• Extraer los subsistemas de un sistema MIMO.

• Especificar puntos de conexión a la hora de interconectar modelos.

InputUnit — Unidades de los canales de entrada

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Unidades de los canales de entrada, especificadas como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una sola entrada.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias entradas.

• '' para no especificar una unidad, para cualquier canal de entrada.

Use InputUnit para especificar las unidades de las señales de entrada. InputUnit no afecta al comportamiento del sistema.

InputGroup — Grupos de canales de entrada

estructura

Grupos de canales de entrada, especificados como una estructura. Use InputGroup para asignar los canales de entrada de un sistema MIMO a grupos y poder referirse a cada uno de los grupos con un nombre. Los nombres de los campos de InputGroup son los nombres de los grupos y los valores de los campos son los canales de entrada de cada grupo. Por ejemplo, puede introducir lo siguiente para crear grupos de entradas llamados controls y noise que incluyan los canales de entrada 1 y 2, y los canales de entrada 3 y 5, respectivamente.

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

Luego, puede usar el siguiente comando para extraer el subsistema de las entradas del grupo controls a todas las salidas.

sys(:,'controls')

De forma predeterminada, InputGroup es una estructura sin campos.

OutputName — Nombres de los canales de salida

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Nombres de los canales de salida, especificados como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una única salida.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias salidas.

• '', para no especificar un nombre, para cualquier canal de salida.

Como alternativa, se pueden asignar nombres a las salidas de un modelo de varias salidas mediante la expansión automática de vectores. Por ejemplo, si sys es un modelo de dos salidas, se puede introducir lo siguiente:

sys.OutputName = 'measurements';

En este caso, el valor se expandirá automáticamente y los nombres de las salidas serán {'measurements(1)';'measurements(2)'}.

También se puede usar la notación abreviada y para hacer referencia a la propiedad OutputName. Por ejemplo, sys.y es equivalente a sys.OutputName.

Utilice OutputName para:

• Identificar los canales en la visualización y las gráficas del modelo.

• Extraer los subsistemas de un sistema MIMO.

• Especificar puntos de conexión a la hora de interconectar modelos.

OutputUnit — Unidades de los canales de salida

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Unidades los canales de salida, especificadas como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una única salida.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias salidas.

• '' para no especificar una unidad, para cualquier canal de salida.

Use OutputUnit para especificar las unidades de las señales de salida. OutputUnit no afecta al comportamiento del sistema.

OutputGroup — Grupos de canales de salida

estructura

Grupos de canales de salida, especificados como una estructura. Use OutputGroup para asignar los canales de salida de un sistema MIMO a grupos y poder referirse a cada uno de los grupos con un nombre. Los nombres de los campos de OutputGroup son los nombres de los grupos y los valores de los campos son los canales de salida de cada grupo. Por ejemplo, puede crear grupos de salidas llamados temperature y measurement que incluyan el canal de salida 1, 3 y los canales de salida 5, respectivamente.

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

Luego, puede usar el siguiente comando para extraer el subsistema de todas las entradas a las salidas del grupo measurement.

sys('measurement',:)

De forma predeterminada, OutputGroup es una estructura sin campos.

Name — Nombre del sistema

'' (predeterminado) | vector de caracteres

Nombre del sistema, especificado como un vector de caracteres. Por ejemplo, 'system_1'.

Notes — Texto especificado por el usuario

{} (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Texto especificado por el usuario que desee asociar con el sistema, especificado como un vector de caracteres, o bien un arreglo de celdas de vectores de caracteres. Por ejemplo, 'System is MIMO'.

UserData — Datos especificados por el usuario

[] (predeterminado) | cualquier tipo de dato de MATLAB^®

Datos especificados por el usuario que desee asociar con el sistema, especificado como cualquier tipo de dato de MATLAB.

SamplingGrid — Cuadrícula de muestreo para arreglos de modelos

arreglo de estructuras

Cuadrícula de muestreo para arreglos de modelos, especificada como un arreglo de estructuras.

Use SamplingGrid para hacer un seguimiento de los valores de las variables asociados con cada uno de los modelos de un arreglo de modelos, incluyendo arreglos de modelos identificados lineales invariantes en el tiempo (IDLTI).

Establezca los nombres de los campos de la estructura como nombres de las variables de muestreo. Establezca los valores de los campos como valores de las variables muestreadas asociadas con cada modelo del arreglo. Todas las variables de muestreo deben ser escalares numéricos y todos los arreglos de valores muestreados deben coincidir con las dimensiones del arreglo de modelos.

Por ejemplo, puede crear un arreglo de modelos lineales de 11 por 1, sysarr, tomando instantáneas de un sistema lineal variante en el tiempo en la unidad de tiempo t = 0:10. El siguiente código almacena las muestras de tiempo junto con los modelos lineales.

 sysarr.SamplingGrid = struct('time',0:10)

Del mismo modo, puede crear un arreglo de modelos de 6 por 9, M, muestreando de forma independiente dos variables, zeta y w. El siguiente código mapea los valores de (zeta,w) a M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

Cuando se visualiza M, cada elemento del arreglo incluye los correspondientes valores zeta y w.

M

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

En el caso de los arreglos de modelos obtenidos por linealización de un modelo de Simulink^® para distintos valores de los parámetros o distintos puntos de funcionamiento, el software rellena SamplingGrid automáticamente con los valores de las variables correspondientes a cada elemento del arreglo. Por ejemplo, los comandos de Simulink Control Design™ linearize (Simulink Control Design) y slLinearizer (Simulink Control Design) rellenan SamplingGrid automáticamente.

De forma predeterminada, SamplingGrid es una estructura sin campos.

Funciones del objeto

Las siguientes listas contienen una muestra representativa de las funciones que se pueden usar con los modelos del tipo tf. En general, cualquier función que se pueda aplicar a modelos de sistemas dinámicos se puede aplicar a un objeto del tipo tf.

Análisis lineales

step	Respuesta al escalón de un sistema dinámico
impulse	Gráfica de la respuesta al impulso del sistema dinámico; datos de la respuesta al impulso
lsim	Calcular datos de simulación de respuesta en el tiempo de un sistema dinámico para entradas arbitrarias
bode	Respuesta en frecuencia de Bode de un sistema dinámico
nyquist	Respuesta de Nyquist de un sistema dinámico
nichols	Respuesta de Nichols de un sistema dinámico
bandwidth	Ancho de banda de respuestas en frecuencia

Análisis de estabilidad

pole	Polos del sistema dinámico
zero	Ceros y ganancia del sistema dinámico SISO
pzplot	Representar un mapa de polos y ceros del sistema dinámico
margin	Margen de ganancia, margen de fase y frecuencias de cruce

Transformación de modelos

zpk	Modelo de cero-polo-ganancia
ss	Modelo de espacio de estados
c2d	Conversión de modelos de tiempo continuo a discreto
d2c	Convertir modelos en tiempo discreto a tiempo continuo
d2d	Remuestreo de modelos de tiempo discreto

Interconexión de modelos

feedback	Conexión de retroalimentación de múltiples modelos
connect	Interconexiones del diagrama de bloques de sistemas dinámicos
series	Conexión en serie de dos modelos
parallel	Conexión paralela de dos modelos

Diseño de controladores

pidtune	Algoritmo de ajuste de PID para un modelo de planta lineal
rlocus	Lugar de las raíces de un sistema dinámico
lqr	Diseño de un regulador lineal cuadrático (LQR)
lqg	Diseño lineal cuadrático gaussiano (LQG)
lqi	Control lineal cuadrático integral
kalman	Diseñar un filtro de Kalman para la estimación de estados

Ejemplos

Modelo de función de transferencia SISO

Para este ejemplo, considere el siguiente modelo de función de transferencia SISO:

$$sys(s)=\frac{1}{2s^2+3s+4}.$$

Especifique los coeficientes del numerador y denominador ordenados en potencias decrecientes de s y cree el modelo de función de transferencia.

numerator = 1;
denominator = [2,3,4];
sys = tf(numerator,denominator)

sys =
 
         1
  ---------------
  2 s^2 + 3 s + 4
 
Continuous-time transfer function.
Model Properties

Modelo de función de transferencia SISO en tiempo discreto

Para este ejemplo, considere el siguiente modelo de función de transferencia SISO en tiempo discreto:

$$sys(z)=\frac{2z}{4z^3+3z-1}.$$

Especifique los coeficientes del numerador y denominador ordenados en potencias decrecientes de z y un tiempo de muestreo de 0,1 segundos. Cree el modelo de función de transferencia en tiempo discreto.

numerator = [2,0];
denominator = [4,0,3,-1];
ts = 0.1;
sys = tf(numerator,denominator,ts)

sys =
 
        2 z
  ---------------
  4 z^3 + 3 z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Función de transferencia de segundo orden a partir de coeficiente de amortiguación y frecuencia natural

Para este ejemplo, considere un modelo de función de transferencia que represente un sistema de segundo orden con una frecuencia natural y un coeficiente de amortiguación conocidos.

La función de transferencia de un sistema de segundo orden, expresada en términos de su coeficiente de amortiguación $$\zeta$$ y su frecuencia natural $${\omega }_0$$, está dada por:

$$sys\left(s\right)=\frac{{\omega }_0^2}{s^2+2\zeta {\omega }_{0}s+{\omega }_0^2}.$$

Suponiendo un coeficiente de amortiguación $$\zeta$$ = 0,25 y una frecuencia natural $${\omega }_0$$ = 3 rad/s, cree la función de transferencia de segundo orden.

zeta = 0.25;
w0 = 3;
numerator = w0^2;
denominator = [1,2*zeta*w0,w0^2];
sys = tf(numerator,denominator)

sys =
 
         9
  ---------------
  s^2 + 1.5 s + 9
 
Continuous-time transfer function.
Model Properties

Analice la respuesta de esta función de transferencia a una entrada de escalón.

stepplot(sys)

La gráfica muestra el ringdown esperado de un sistema de segundo orden con bajo coeficiente de amortiguación.

Modelo de función de transferencia MIMO en tiempo discreto

Cree una función de transferencia para el siguiente modelo en tiempo discreto con múltiples entradas y múltiples salidas:

$$sys\left(z\right)=\left[\begin{array}{cc}\frac{1}{z+0.3}& \frac{z}{z+0.3}\\ \frac{-z+2}{z+0.3}& \frac{3}{z+0.3}\end{array}\right]$$

con tiempo de muestreo de ts = 0.2 segundos.

Especifique los coeficientes del numerador como una matriz de 2 por 2.

numerators = {1 [1 0];[-1 2] 3};

Especifique los coeficientes del denominador común como un vector fila.

denominator = [1 0.3];

Cree el modelo de función de transferencia MIMO en tiempo discreto.

ts = 0.2;
sys = tf(numerators,denominator,ts)

sys =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

Para más información sobre la creación de funciones de transferencia MIMO, consulte Funciones de transferencia MIMO.

Concatenación de funciones de transferencia SISO en un modelo de función de transferencia MIMO

Para este ejemplo, cree un modelo de función de transferencia MIMO a partir de la concatenación de modelos de función de transferencia SISO. Considere la siguiente función de transferencia de una entrada y dos salidas:

$$sys(s)=\left[\begin{array}{c}\frac{s-1}{s+1}\\ \frac{s+2}{s^2+4s+5}\end{array}\right].$$

Especifique el modelo de función de transferencia MIMO a partir de la concatenación de las entradas SISO.

sys1 = tf([1 -1],[1 1]);		
sys2 = tf([1 2],[1 4 5]);
sys = [sys1;sys2]

sys =
 
  From input to output...
       s - 1
   1:  -----
       s + 1
 
           s + 2
   2:  -------------
       s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

Para más información sobre la creación de funciones de transferencia MIMO, consulte Funciones de transferencia MIMO.

Modelo de función de transferencia a partir de expresión racional

Para este ejemplo, cree un modelo de función de transferencia en tiempo continuo usando expresiones racionales. A veces, usar una expresión racional es más simple e intuitivo que especificar los coeficientes polinomiales del numerador y del denominador.

Considere el siguiente sistema:

$$sys(s)=\frac{s}{s^2+2s+10}.$$

Para crear el modelo de función de transferencia, primero especifique s como un objeto tf.

s = tf('s')

s =
 
  s
 
Continuous-time transfer function.
Model Properties

Cree el modelo de función de transferencia usando s en la expresión racional.

sys = s/(s^2 + 2*s + 10)

sys =
 
        s
  --------------
  s^2 + 2 s + 10
 
Continuous-time transfer function.
Model Properties

Modelo de función de transferencia en tiempo discreto a partir de expresión racional

Para este ejemplo, cree un modelo de función de transferencia en tiempo discreto usando una expresión racional. A veces, usar una expresión racional es más fácil e intuitivo que especificar los coeficientes polinomiales.

Considere el siguiente sistema:

$$sys(z)=\frac{z-1}{z^2-1.85z+0.9}.$$

Para crear el modelo de función de transferencia, primero especifique z como un objeto tf y el tiempo de muestreo Ts.

ts = 0.1;
z = tf('z',ts)

z =
 
  z
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Cree el modelo de función de transferencia usando z en la expresión racional.

sys = (z - 1) / (z^2 - 1.85*z + 0.9)

sys =
 
        z - 1
  ------------------
  z^2 - 1.85 z + 0.9
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Modelo de función de transferencia con propiedades heredadas

Para este ejemplo, cree un modelo de función de transferencia con propiedades heredadas de otro modelo de función de transferencia. Considere las siguientes dos funciones de transferencia:

$$sys1(s)=\frac{2s}{s^2+8s}andsys2(s)=\frac{s-1}{7s^4+2s^3+9}.$$

Para este ejemplo, cree un modelo sys1 con las propiedades TimeUnit y InputDelay definidas en 'minutes'.

numerator1 = [2,0];
denominator1 = [1,8,0];
sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')

sys1 =
 
     2 s
  ---------
  s^2 + 8 s
 
Continuous-time transfer function.
Model Properties

propValues1 = [sys1.TimeUnit,sys1.InputUnit]

propValues1 = 1×2 cell
    {'minutes'}    {'minutes'}

Cree el segundo modelo de función de transferencia con propiedades heredadas de sys1.

numerator2 = [1,-1];
denominator2 = [7,2,0,0,9];
sys2 = tf(numerator2,denominator2,sys1)

sys2 =
 
        s - 1
  -----------------
  7 s^4 + 2 s^3 + 9
 
Continuous-time transfer function.
Model Properties

propValues2 = [sys2.TimeUnit,sys2.InputUnit]

propValues2 = 1×2 cell
    {'minutes'}    {'minutes'}

Observe que el modelo de función de transferencia sys2 tiene las mismas propiedades que sys1.

Arreglo de modelos de función de transferencia

Puede usar un bucle for para especificar un arreglo de modelos de función de transferencia.

En primer lugar, predefina el arreglo de funciones de transferencia con ceros.

sys = tf(zeros(1,1,3));

Los primeros dos índices representan el número de salidas y entradas de los modelos, en tanto que el tercer índice representa el número de modelos en el arreglo.

Cree el arreglo de modelo de función de transferencia usando una expresión racional en el bucle for.

s = tf('s');                                                  
for k = 1:3                                                             
    sys(:,:,k) = k/(s^2+s+k);                                          
end
sys

sys(:,:,1,1) =
 
       1
  -----------
  s^2 + s + 1
 

sys(:,:,2,1) =
 
       2
  -----------
  s^2 + s + 2
 

sys(:,:,3,1) =
 
       3
  -----------
  s^2 + s + 3
 
3x1 array of continuous-time transfer functions.
Model Properties

Conversión de un modelo de espacio de estados en una función de transferencia

Para este ejemplo, calcule la función de transferencia del siguiente modelo de espacio de estados:

$$A=\left[\begin{array}{cc}-2& -1\\ 1& -2\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ 2& -1\end{array}\right],C=\left[\begin{array}{cc}1& 0\end{array}\right],D=[\begin{array}{cc}0& 1\end{array}].$$

Cree el modelo de espacio de estados usando las matrices de espacio de estados.

A = [-2 -1;1 -2];
B = [1 1;2 -1];
C = [1 0];
D = [0 1];
ltiSys = ss(A,B,C,D);

Convierta el modelo de espacio de estados ltiSys en una función de transferencia.

sys = tf(ltiSys)

sys =
 
  From input 1 to output:
        s
  -------------
  s^2 + 4 s + 5
 
  From input 2 to output:
  s^2 + 5 s + 8
  -------------
  s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

Extracción de funciones de transferencia de un modelo identificado

Para este ejemplo, extraiga los componentes medidos y de ruido de un modelo polinomial identificado en dos funciones de transferencia independientes.

Cargue el modelo polinomial Box-Jenkins ltiSys en identifiedModel.mat.

load('identifiedModel.mat','ltiSys');

ltiSys es un modelo identificado en tiempo discreto con el formato: $$y(t)=\frac{B}{F}u(t)+\frac{C}{D}e(t)$$, donde $$\frac{B}{F}$$ representa el componente medido y $$\frac{C}{D}$$, el componente de ruido.

Extraiga el componente medido y el componente de ruido como funciones de transferencia.

sysMeas = tf(ltiSys,'measured') 

sysMeas =
 
  From input "u1" to output "y1":
            -0.1426 z^-1 + 0.1958 z^-2
  z^(-2) * ----------------------------
           1 - 1.575 z^-1 + 0.6115 z^-2
 
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

sysNoise = tf(ltiSys,'noise')

sysNoise =
 
  From input "v@y1" to output "y1":
           0.04556 + 0.03301 z^-1
  ----------------------------------------
  1 - 1.026 z^-1 + 0.26 z^-2 - 0.1949 z^-3
 
Input groups:        
    Name     Channels
    Noise       1    
                     
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

El componente medido puede servir como modelo de planta, mientras que el componente de ruido puede usarse como modelo de perturbaciones para el diseño de un sistema de control.

Especificación de los nombre de las entradas y las salidas en un modelo de función de transferencia MIMO

Los objetos de modelos de función de transferencia incluyen datos sobre el modelo que ayudan a recordar qué representa el modelo. Por ejemplo, se pueden asignar nombres a las entradas y salidas del modelo.

Considere el siguiente modelo de función de transferencia MIMO en tiempo continuo:

$$sys(s)=\left[\begin{array}{c}\frac{s+1}{s^2+2s+2}\\ \frac{1}{s}\end{array}\right]$$

El modelo tiene una entrada, $$-$$ Current, y dos salidas, $$-$$ Torque y Angular velocity.

En primer lugar, especifique los coeficientes del numerador y denominador del modelo.

numerators = {[1 1] ; 1};
denominators = {[1 2 2] ; [1 0]};

Cree el modelo de función de transferencia especificando el nombre de la entrada y los nombres de las salidas.

sys = tf(numerators,denominators,'InputName','Current',...
        'OutputName',{'Torque' 'Angular Velocity'})

sys =
 
  From input "Current" to output...
                s + 1
   Torque:  -------------
            s^2 + 2 s + 2
 
                      1
   Angular Velocity:  -
                      s
 
Continuous-time transfer function.
Model Properties

Especificación del orden de los polinomios en una función de transferencia en tiempo discreto

Para este ejemplo, especifique el orden de los polinomios en modelos de función de transferencia en tiempo discreto mediante la propiedad 'Variable'.

Considere las siguientes funciones de transferencia en tiempo discreto con un tiempo de muestreo de 0,1 segundos:

$$sys1(z)=\frac{z^2}{z^2+2z+3}sys2(z^{-1})=\frac{1}{1+2z^{-1}+3z^{-2}}.$$

Cree la primera función de transferencia en tiempo discreto especificando los coeficientes de z.

numerator = [1,0,0];
denominator = [1,2,3];
ts = 0.1;
sys1 = tf(numerator,denominator,ts)

sys1 =
 
       z^2
  -------------
  z^2 + 2 z + 3
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Los coeficientes de sys1 están ordenados en potencias decrecientes de z.

tf cambia la convención en función del valor de la propiedad 'Variable'. Dado que sys2 es el modelo de función de transferencia inverso de sys1, especifique 'z^-1' como 'Variable' y use los mismos coeficientes del numerador y denominador.

sys2 = tf(numerator,denominator,ts,'Variable','z^-1')

sys2 =
 
           1
  -------------------
  1 + 2 z^-1 + 3 z^-2
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Ahora, los coeficientes de sys2 están ordenados en potencias crecientes de z^-1.

Basándose en las diferentes convenciones, puede especificar el orden de los polinomios en los modelos de función de transferencia mediante la propiedad 'Variable'.

Filtro paso bajo ajustable

En este ejemplo, deberá crear un filtro paso bajo con un parámetro ajustable a:

$$F=\frac{a}{s+a}$$

Dado que los coeficientes del numerador y denominador de un bloque tunableTF son independientes, no puede usar tunableTF para representar F. En su lugar, genere F con el objeto de parámetro real ajustable realp.

Cree un parámetro real ajustable con un valor inicial de 10.

a = realp('a',10)

a = 
       Name: 'a'
      Value: 10
    Minimum: -Inf
    Maximum: Inf
       Free: 1

Real scalar parameter.

Use tf para crear el filtro paso bajo ajustable F.

numerator = a;
denominator = [1,a];
F = tf(numerator,denominator)

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

F es un objeto de tipo genss que tiene el parámetro ajustable a en su propiedad Blocks. Se puede conectar F con otros modelos ajustables o numéricos para crear modelos de sistemas de control más complejos. Para ver un ejemplo, consulte Sistema de control con componentes ajustables.

Modelo de función de transferencia MIMO de ganancia estática

En este ejemplo, creará un modelo de función de transferencia MIMO de ganancia estática.

Considere la siguiente matriz de ganancia estática de dos entradas y dos salidas, m:

$$m=\left[\begin{array}{cc}2& 4\\ 3& 5\end{array}\right]$$

Especifique la matriz de ganancia y cree el modelo de función de transferencia de ganancia estática.

m = [2,4;...
    3,5];
sys1 = tf(m)

sys1 =
 
  From input 1 to output...
   1:  2
 
   2:  3
 
  From input 2 to output...
   1:  4
 
   2:  5
 
Static gain.
Model Properties

Puede usar el modelo de función de transferencia de ganancia estática sys1 obtenido arriba y ponerlo en cascada con otro modelo de función de transferencia.

Para hacerlo, cree otro modelo de función de transferencia discreta de dos entradas y dos salidas y use la función series para conectar ambos modelos.

numerators = {1,[1,0];[-1,2],3};
denominator = [1,0.3];
ts = 0.2;
sys2 = tf(numerators,denominator,ts)

sys2 =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

sys = series(sys1,sys2)

sys =
 
  From input 1 to output...
       3 z^2 + 2.9 z + 0.6
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -2 z^2 + 12.4 z + 3.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
  From input 2 to output...
       5 z^2 + 5.5 z + 1.2
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -4 z^2 + 21.8 z + 6.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

Calcular aproximación de función de transferencia truncada de modelo disperso

Desde R2025a

Este ejemplo muestra cómo obtener un modelo de función de transferencia truncada de un modelo de espacio de estados disperso. Este ejemplo utiliza un modelo disperso obtenido linealizando un modelo térmico de distribución de calor en una varilla cilíndrica circular.

Cargue los datos del modelo.

load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)

Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.

Analice la respuesta en frecuencia del modelo.

sigmaplot(sys,w)

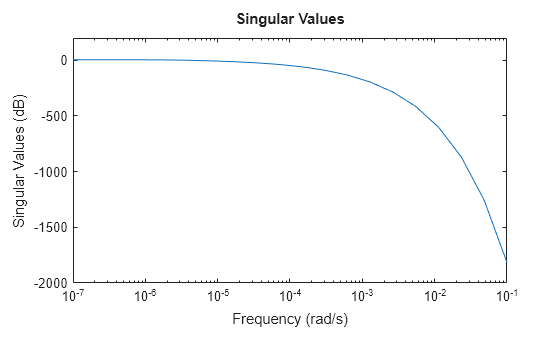
Para obtener una aproximación truncada, utilice tf y especifique la banda de frecuencia de enfoque. Para este modelo, puede usar un rango de frecuencia de 0 rad/s a 0,01 rad/s para obtener la aproximación de orden inferior.

tsys = tf(sys,Focus=[0 1e-2],Display="off");

Compare la respuesta en frecuencia.

sigmaplot(sys,tsys,w)

Este modelo térmico tiene una atenuación muy pronunciada más allá de 0,001 rad/s. De forma predeterminada, el modelo reducido obtenido usando tf no proporciona una buena coincidencia para esta atenuación. Para mitigarlo, puede utilizar el argumento RollOff de tf y especificar un valor de atenuación mínimo más allá de la banda de frecuencia de enfoque. Especifique un valor de pendiente de atenuación de -45, que corresponde a una tasa de al menos –900 db/década.

tsys2 = tf(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,tsys2,w)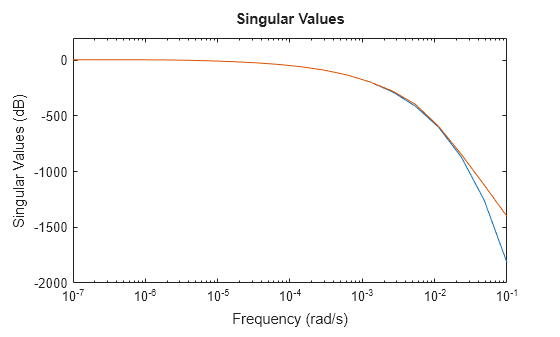

El modelo reducido ahora proporciona una aproximación mucho mejor del valor de atenuación. Sin embargo, en este ejemplo, reajustar la pendiente de atenuación usando tf requiere volver a calcular ceros y polos. Esto puede demandar una alta carga computacional en caso de modelos a gran escala. Como alternativa, puede utilizar el método de truncamiento de polos y ceros de reducespec y ajustar la atenuación sin coste de cálculo adicional, después de que el software haya calculado los polos y ceros. Para ver un ejemplo, consulte Zero-Pole Truncation of Thermal Model.

Limitaciones

• Los modelos de función de transferencia son poco adecuados para el cálculo numérico. Una vez creados, conviértalos a representaciones en espacio de estados antes de combinarlos con otros modelos o realizar transformaciones de modelos. Luego, puede convertir los modelos resultantes nuevamente en funciones de transferencia para revisarlos.

• Un modelo no lineal identificado no puede convertirse directamente en un modelo de función de transferencia mediante la función tf. Para obtener un modelo de función de transferencia:

  1. Convierta el modelo no lineal identificado en un modelo LTI identificado con las funciones linapp (System Identification Toolbox), idnlarx/linearize (System Identification Toolbox) o idnlhw/linearize (System Identification Toolbox).

  2. Luego, convierta el modelo resultante en un modelo de función de transferencia mediante la función tf.

Algoritmos

Para convertir modelos dispersos, tf utiliza el algoritmo Krylov--Schur [1] para que las iteraciones de potencia inversa calculen polos y ceros en la banda de frecuencia especificada.

Referencias

[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.

Historial de versiones

Introducido antes de R2006a

R2025a: Calcular aproximación de función de transferencia truncada de modelos dispersos

Ahora, puede usar tf para convertir modelos de espacio de estados dispersos y obtener una aproximación de función de transferencia truncada. tf calcula un subconjunto de los ceros y polos de modelos dispersos, normalmente en una banda de frecuencia baja específica [0 f_max]. Esto puede producir mejores aproximaciones de frecuencia baja que la reducción del orden del modelo por truncamiento modal, a expensas de más cálculos. tf también proporciona control directo sobre la pendiente de atenuación más allá de la frecuencia f_max. Utilice la nueva sintaxis tsys = tf(sparseSys,Name=Value) para obtener una aproximación basada en opciones especificadas, como el rango de frecuencia de enfoque. Para ver un ejemplo, consulte Calcular aproximación de función de transferencia truncada de modelo disperso.

Consulte también

filt | frd | get | set | ss | tfdata | zpk | genss | realp | genmat | tunableTF

Temas

• What Are Model Objects?
• Funciones de transferencia
• Modelos numéricos de tiempo discreto
• Funciones de transferencia MIMO
• Using the Right Model Representation
• Uso de FEEDBACK para cerrar lazos de retroalimentación

Sitios web externos

• Análisis de la función de transferencia de sistemas dinámicos (Recursos para enseñanza de MathWorks)