La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

zpk

Modelo de cero-polo-ganancia

Descripción

Use zpk para crear modelos de cero-polo-ganancia o para convertir modelos de sistemas dinámicos al formato de modelo de cero-polo-ganancia.

Los modelos de cero-polo-ganancia son una representación de funciones de transferencia de forma factorizada. Por ejemplo, considere la siguiente función de transferencia SISO de tiempo continuo:

$$G\left(s\right)=\frac{s^2-3s-4}{s^2+5s+6}$$

G(s) puede factorizarse en formato de cero-polo-ganancia como:

$$G\left(s\right)=\frac{\left(s+1\right)\left(s-4\right)}{\left(s+2\right)\left(s+3\right)}.$$

Una representación más general del modelo de cero-polo-ganancia SISO es la siguiente:

$$h\left(s\right)=k\frac{\left(s-z\left(1\right)\right)\left(s-z\left(2\right)\right)\dots \left(s-z\left(m\right)\right)}{\left(s-p\left(1\right)\right)\left(s-p\left(2\right)\right)\dots \left(s-p\left(n\right)\right)}$$

En este caso, z y p son los vectores de ceros y polos de valores reales o complejos, y k es la ganancia escalar de valores reales o complejos. Para los modelos MIMO, cada canal de E/S está representado por una de esas funciones de transferencia h_ij(s).

Para crear un objeto de modelo de cero-polo-ganancia, puede especificar los polos, los ceros y la ganancia directamente o convertir un modelo de otro tipo (por ejemplo, un modelo de espacio de estados ss) al formato de cero-polo-ganancia.

También puede usar zpk para crear modelos generalizados de espacio de estados (genss) o modelos de espacio de estados con incertidumbre (uss (Robust Control Toolbox)).

Creación

Sintaxis

sys = zpk(zeros,poles,gain)

sys = zpk(zeros,poles,gain,ts)

sys = zpk(zeros,poles,gain,ltiSys)

sys = zpk(m)

sys = zpk(___,PropertyName=Value)

sys = zpk(ltiSys)

sys = zpk(ltiSys,Name=Value)

sys = zpk(ltiSys,component)

s = zpk('s')

z = zpk('z',ts)

Descripción

Crear el modelo de ZPK

sys = zpk(zeros,poles,gain) crea un modelo de cero-polo-ganancia de tiempo continuo con zeros y poles especificados como vectores y el valor escalar de gain. La salida sys es un objeto de modelo zpk que almacena los datos del modelo. Establezca zeros o poles en [] para sistemas sin ceros ni polos. No es necesario que estas dos entradas tengan la misma longitud ni que el modelo sea propio (es decir, que tenga un exceso de polos).

sys = zpk(zeros,poles,gain,ts) crea un modelo de cero-polo-ganancia de tiempo discreto con tiempo de muestreo ts. Establezca ts en -1 o [] si no desea especificar el tiempo de muestreo.

sys = zpk(zeros,poles,gain,ltiSys) crea un modelo de cero-polo-ganancia con propiedades herdadas del modelo de sistema dinámico ltiSys, incluido el tiempo de muestreo.

sys = zpk(m) crea un modelo de cero-polo-ganancia que representa la ganancia estática m.

sys = zpk(___,PropertyName=Value) establece las propiedades Propiedades del modelo de cero-polo-ganancia usando uno o más argumentos nombre-valor para establecer propiedades adicionales del modelo. Esta sintaxis funciona con cualquiera de las combinaciones de entrada/argumento anteriores.

Convertir al modelo de ZPK

sys = zpk(ltiSys) convierte el modelo de sistema dinámico ltiSys en un modelo de cero-polo-ganancia.

sys = zpk(ltiSys,Name=Value) obtiene una representación zpk truncada del modelo disperso ltiSys calculando ceros y polos en función de uno o más argumentos nombre-valor especificados. Dado que este método calcula ceros para cada par entrada-salida, es más adecuado para modelos con tamaños de entrada-salida pequeños. (desde R2025a)

sys = zpk(ltiSys,component) convierte el componente component especificado de ltiSys al formato de cero-polo-ganancia. Use esta sintaxis solo si ltiSys es un modelo identificado lineal invariante en el tiempo (LTI), como un modelo idss o idtf.

Crear una variable para una expresión racional

s = zpk('s') crea una variable especial s que puede usar en una expresión racional para crear un modelo de cero-polo-ganancia de tiempo continuo. En ocasiones, usar una expresión racional es más fácil e intuitivo que especificar los coeficientes de los polinomios.

z = zpk('z',ts) crea una variable especial z que puede usar en una expresión racional para crear un modelo de cero-polo-ganancia de tiempo discreto. Si no desea especificar el tiempo de muestreo, el argumento de entrada ts se debe establecer en -1.

Argumentos de entrada

zeros — Ceros del modelo de cero-polo-ganancia

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Ceros del modelo de cero-polo-ganancia, especificados como:

• Un vector fila para modelos SISO. Por ejemplo, use [1,2+i,2-i] para crear un modelo con ceros en s = 1, s = 2+i y s = 2-i. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia SISO de tiempo continuo.

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar un modelo de cero-polo-ganancia MIMO, donde Ny es el número de salidas y Nu es el número de entradas. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia MIMO de tiempo discreto.

Por ejemplo, si a es un parámetro ajustable realp con valor nominal 3, puede utilizar zeros = [1 2 a] para crear un modelo genss con ceros en s = 1 y s = 2, y un cero ajustable en s = 3.

Cuando utiliza este argumento de entrada para crear un modelo zpk, el argumento establece el valor inicial de la propiedad Z.

poles — Polos del modelo de cero-polo-ganancia

vector fila | Arreglo de celdas de vectores fila de Ny por Nu

Polos del modelo de cero-polo-ganancia, especificados como:

• Un vector fila para modelos SISO. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia SISO de tiempo continuo.

• Un arreglo de celdas de vectores fila de Ny por Nu para especificar un modelo de cero-polo-ganancia MIMO, donde Ny es el número de salidas y Nu es el número de entradas. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia MIMO de tiempo discreto.

También es una propiedad del objeto zpk. Este argumento de entrada establece el valor inicial de la propiedad P.

gain — Ganancia del modelo de cero-polo-ganancia

escalar | Matriz de Ny por Nu

Ganancia del modelo de cero-polo-ganancia, especificada como:

• Un escalar para modelos SISO. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia SISO de tiempo continuo.

• Una matriz de Ny por Nu para especificar un modelo de cero-polo-ganancia MIMO, donde Ny es el número de salidas y Nu es el número de entradas. Para ver un ejemplo, consulte Modelo de cero-polo-ganancia MIMO de tiempo discreto.

También es una propiedad del objeto zpk. Este argumento de entrada establece el valor inicial de la propiedad K.

ts — Tiempo de muestreo

escalar

Tiempo de muestreo, especificado como un escalar. También es una propiedad del objeto zpk. Este argumento de entrada establece el valor inicial de la propiedad Ts.

ltiSys — Sistema dinámico

modelo de sistema dinámico | arreglo de modelos

Sistema dinámico, especificado como un modelo de sistema dinámico SISO o MIMO, o bien un arreglo de modelos de sistemas dinámicos. Se admiten los siguientes tipos de sistemas dinámicos:

• Modelos LTI numéricos de tiempo continuo o de tiempo discreto, como modelos tf, zpk, ss o pid.

  Si ltiSys es un modelo de espacio de estados disperso (sparss o mechss), el software calcula una aproximación de cero-polo-ganancia truncada en una banda de frecuencia específica de enfoque. Para los modelos dispersos, utilice los argumentos nombre-valor para especificar las opciones de cálculo. Si no especifica ninguna opción, el software calcula los primeros 1.000 polos y ceros con menor magnitud. Además, obtener una aproximación de cero-polo-ganancia truncada solo es aplicable a modelos con una representación de sparss válida. (desde R2025a)

• Modelos LTI generalizados o con incertidumbre, como modelos genss o uss (Robust Control Toolbox). (El uso de modelos con incertidumbre requiere una licencia de Robust Control Toolbox™).

  El modelo de cero-polo-ganancia resultante asume que

  • valores actuales de los componentes ajustables para los bloques de diseño de control ajustables.

  • valores nominales del modelo para los bloques de diseño de control con incertidumbre.

• Modelos LTI identificados, como modelos idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox) y idgrey (System Identification Toolbox). Para seleccionar el componente del modelo identificado que desea convertir, especifique component. Si no especifica component, el comportamiento predeterminado de tf es convertir el componente medido del modelo identificado. El uso de modelos identificados requiere System Identification Toolbox™.

  Un modelo no lineal identificado no puede convertirse en un objeto de modelo zpk. Puede utilizar primero funciones de aproximación lineal, como linearize y linapp (esta funcionalidad requiere System Identification Toolbox).

m — Ganancia estática

escalar | matriz

Ganancia estática, especificada como un escalar o una matriz. La ganancia estática o ganancia de estado estacionario de un sistema representa la relación entre la salida y la entrada en régimen estacionario.

component — Componente del modelo identificado

'measured' (predeterminado) | 'noise' | 'augmented'

Componente del modelo identificado que se desea convertir, especificado con una de las siguientes opciones:

• 'measured': convierte el componente medido de sys.

• 'noise': convierte el componente de ruido de sys

• 'augmented': convierte tanto el componente medido como el componente de ruido de sys.

component solo es válido cuando sys es un modelo LTI identificado.

Para más información acerca de los modelos LTI identificados y sus componentes medidos y de ruido, consulte Identified LTI Models.

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos nombre-valor deben aparecer después de los otros argumentos, aunque el orden de los pares no es importante.

Ejemplo: sys = zpk(sparseSys,Focus=[0 100],Display="off")

UseParallel — Usar el cálculo paralelo

0 o false (predeterminado) | 1 o true

Desde R2025a

Uso de cálculo paralelo durante el cálculo de polos y ceros, especificado como un 0 numérico o lógico (false) o 1 (true).

Cuando UseParallel se establece en true, puede elegir explícitamente escalar a su entorno paralelo preferido. Permitir el cálculo paralelo puede dar como resultado un mejor rendimiento durante el cálculo de polos y ceros. Sin embargo, incluso si se establece UseParallel en false, el algoritmo puede usar el multihilo integrado para aprovechar al máximo los recursos locales. Para obtener más información, consulte MATLAB Multicore.

Esta opción requiere una licencia de Parallel Computing Toolbox™.

RollOff — Pendiente de atenuación

0 (predeterminado) | escalar no positivo | matriz

Desde R2025a

Pendiente de atenuación, especificada como una matriz o un escalar no positivo.

• Utilice un valor escalar para los modelos SISO o cuando la pendiente sea uniforme para todos los pares entrada-salida de los modelos MIMO.

• Utilice una matriz cuando la pendiente sea diferente para cada par entrada-salida de los modelos MIMO.

Esta opción le permite especificar cómo debe atenuar la aproximación más allá del rango de frecuencia especificado. Por ejemplo, Slope de -2 garantiza que la ganancia se desplace a una tasa de al menos –40 dB/década (la tasa de atenuación de 1/s²) más allá de fmax.

Focus — Rango de frecuencia de interés

[0 Inf] (predeterminado) | vector

Desde R2025a

Rango de frecuencia de interés, especificado como un vector con la forma [0,fmax]. Cuando se especifica un rango de frecuencia de enfoque, el software calcula solo los polos con frecuencia natural en este rango. Para los modelos de tiempo discreto, el software aproxima la frecuencia natural equivalente a través de la transformada de Tustin.

Dado que zpk calcula todos los polos y ceros en el rango de frecuencia especificado, normalmente se especifica un rango de frecuencia baja para limitar el cálculo de una gran cantidad de polos y ceros. De forma predeterminada, el foco no está especificado ([0 Inf]) y el algoritmo calcula hasta MaxNumber polos y ceros.

MaxNumber — Número máximo de polos y ceros a calcular

1000 (predeterminado) | entero positivo

Desde R2025a

Número máximo de polos y ceros a calcular, especificado como un entero positivo. Este valor limita el número de polos y ceros calculados por el algoritmo y el orden de aproximación del modelo disperso original.

Shift — Desplazamiento espectral

0 (predeterminado) | escalar finito

Desde R2025a

Desplazamiento espectral, especificado como un escalar finito.

El software calcula los polos con la frecuencia natural en el rango especificado [0,fmax] utilizando iteraciones de potencia inversa para A-sigma*E, lo que obtiene valores propios más cercanos al desplazamiento sigma. Cuando A es singular y sigma es cero, el algoritmo falla porque no existe una inversa. Por lo tanto, para los modelos dispersos con acción integral (s = 0 o z = 1 para modelos de tiempo discreto), puede utilizar esta opción para desplazar implícitamente los polos o ceros al valor más cercano a este valor de desplazamiento. Especifique un valor de desplazamiento que no sea igual a un polo existente o al valor cero del modelo original.

Tolerance — Precisión de los polos y ceros calculados

1e-12 (predeterminado) | escalar finito positivo

Desde R2025a

Tolerancia de precisión de los polos y ceros calculados, especificada como un escalar finito positivo. Este valor controla la convergencia de los valores propios calculados en iteraciones de potencia inversa.

Display — Mostrar u ocultar el informe de progreso

"on" (predeterminado) | "off"

Desde R2025a

Mostrar u ocultar el informe de progreso, especificado como "off" o "on".

Argumentos de salida

sys — Modelo de sistema de salida

Objeto de modelo zpk | Objeto de modelo genss | Objeto de modelo uss

Modelo de sistema de salida, en uno de los siguientes formatos:

• Un objeto de modelo de cero-polo-ganancia (zpk), cuando los argumentos de entrada zeros, poles y gain contienen valores numéricos. sys siempre es un objeto de modelo zpk cuando se convierte ltiSys al tipo de modelo zpk.

• Un objeto de modelo de espacio de estados generalizado (genss), cuando los argumentos de entrada zeros, poles y gain incluyen parámetros ajustables, como parámetros realp o matrices generalizadas (genmat).

• Un objeto de modelo de espacio de estados con incertidumbre (uss), cuando los argumentos de entrada zeros, poles y gain incluyen parámetros con incertidumbre. El uso de modelos con incertidumbre requiere una licencia de Robust Control Toolbox.

Propiedades

Z — Ceros del sistema

arreglo de celdas | Arreglo de celdas de vectores fila de Ny por Nu

Ceros del sistema, especificados como:

• Un arreglo de celdas de ceros de función de transferencia o las raíces del numerador para modelos SISO.

• Un arreglo de celdas de vectores fila de Ny por Nu de los ceros para cada par E/S en un modelo MIMO, donde Ny es el número de salidas y Nu es el número de entradas.

Los valores de Z pueden ser reales o complejos.

P — Polos del sistema

arreglo de celdas | Arreglo de celdas de vectores fila de Ny por Nu

Polos del sistema, especificados como:

• Un arreglo de celdas de polos de función de transferencia o las raíces del denominador para modelos SISO.

• Un arreglo de celdas de vectores fila de Ny por Nu de los polos para cada par E/S en un modelo MIMO, donde Ny es el número de salidas y Nu es el número de entradas.

Los valores de P pueden ser reales o complejos.

K — Ganancia del sistema

escalar | Matriz de Ny por Nu

Ganancia del sistema, especificada como:

• Un valor escalar para modelos SISO.

• Una matriz de Ny por Nu que almacena los valores para cada par E/S del modelo MIMO, donde Ny es el número de salidas y Nu es el número de entradas.

Los valores de K pueden ser reales o complejos.

DisplayFormat — Especifica cómo los polinomios del numerador y denominador se factorizan para su visualización

'roots' (predeterminado) | 'frequency' | 'time constant'

Especifica cómo los polinomios del numerador y denominador se factorizan para su visualización, especificados como una de las siguientes opciones:

• 'roots': muestre factores en términos de la ubicación de las raíces de los polinomios. 'roots' es el valor predeterminado de DisplayFormat.

• 'frequency': muestra los factores en cuanto a frecuencias naturales de la raíz ω₀ y coeficientes de amortiguación ζ.

  El formato de visualización 'frequency' no está disponible para modelos de tiempo discreto con valor Variable 'z^-1' o 'q^-1'.

• 'time constant': muestra los factores en cuanto a tiempo de la raíz τ y coeficientes de amortiguación ζ.

  El formato de visualización 'time constant' no está disponible para modelos de tiempo discreto con valor Variable 'z^-1' o 'q^-1'.

Para modelos de tiempo continuo, la siguiente tabla muestra cómo los factores de polinomios se organizan en cada formato de visualización.

Valor DisplayName	Factor de primer orden (raíz real $$R$$)	Factor de segundo orden (par de raíces complejas $$R=a\pm jb$$)
'roots'	$$(s-R)$$	$$(s^2-\alpha s+\beta ),$$ donde $$\alpha =2a,\beta =a^2+b^2$$
'frequency'	$$\left(1-\frac{s}{{\omega }_0}\right),$$ donde $${\omega }_0=R$$	$$1-2\zeta \left(\frac{s}{{\omega }_0}\right)+{\left(\frac{s}{{\omega }_0}\right)}^2,$$ donde $${\omega }_0{}^2=a^2+b^2,\zeta =\frac{a}{{\omega }_0}$$
'time constant'	$$\left(1-\tau s\right),$$ donde $$\tau =\frac{1}{R}$$	$$1-2\zeta \left(\tau s\right)+{\left(\tau s\right)}^2,$$ donde $$\tau =\frac{1}{{\omega }_0},\zeta =a\tau$$

Para modelos de tiempo discreto, los factores de polinomios se organizan de forma similar a como ocurre en los modelos de tiempo continuo, con las siguientes sustituciones de variables:

$$s\to w=\frac{z-1}{T_s};R\to \frac{R-1}{T_s},$$

donde T_s es el tiempo de muestreo. En tiempo discreto, τ y ω₀ se ajustan con precisión a la constante de tiempo y la frecuencia natural de la raíz de tiempo continuo equivalente, siempre que se cumplan las siguientes condiciones: $$\left|z-1\right|<<T_s\left({\omega }_0<<\frac{\pi }{T_s}=\text{Nyquist frequency}\right)$$.

Variable — Variable de visualización del modelo de cero-polo-ganancia

's' (predeterminado) | 'z' | 'p' | 'q' | 'z^-1' | 'q^-1'

Variable de visualización del modelo de cero-polo-ganancia, especificada como una de las siguientes opciones:

• 's': la opción predeterminada para modelos de tiempo continuo

• 'z': la opción predeterminada para modelos de tiempo discreto

• 'p': equivalente a 's'

• 'q': equivalente a 'z'

• 'z^-1': la inversa de 'z'

• 'q^-1': equivalente a 'z^-1'

IODelay — Retardo de transporte

0 (predeterminado) | escalar | Arreglo de Ny por Nu

Retardo de transporte, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de transporte de un sistema SISO, o bien un retardo de transporte común a todos los pares entrada-salida de un sistema MIMO.

• Arreglo de Ny por Nu: especifica retardos de transporte independientes para cada par entrada-salida de un sistema MIMO. Aquí, Ny es el número de salidas y Nu es el número de entradas.

Si se trata de un sistema de tiempo continuo, los retardos de transporte se deben especificar en las unidades dadas por la propiedad TimeUnit. Si se trata de un sistema de tiempo discreto, los retardos de transporte se deben especificar como múltiplos enteros del tiempo de muestreo, Ts. Para más información sobre el retardo de tiempo, consulte Retardos de tiempo en sistemas lineales.

InputDelay — Retardo de entrada

0 (predeterminado) | escalar | Vector de Nu por 1

Retardo de entrada para cada canal de entrada, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de entrada de un sistema SISO, o bien un retardo común a todas las entradas de un sistema con varias entradas.

• Vector de Nu por 1: especifica retardos de entrada independientes para cada entrada de un sistema con varias entradas, donde Nu es el número de entradas.

Si se trata de un sistema de tiempo continuo, los retardos de entrada se deben especificar en las unidades dadas por la propiedad TimeUnit. Si se trata de un sistema de tiempo discreto, los retardos de entrada se deben especificar como múltiplos enteros del tiempo de muestreo, Ts.

Para más información, consulte Retardos de tiempo en sistemas lineales.

OutputDelay — Retardo de salida

0 (predeterminado) | escalar | Vector de Ny por 1

Retardo de salida para cada canal de salida, especificado como una de las siguientes opciones:

• Escalar: especifica el retardo de salida de un sistema SISO, o bien un retardo común a todas las salidas de un sistema con varias salidas.

• Vector de Ny por 1: especifica retardos de salida independientes para cada salida de un sistema con varias salidas, donde Ny es el número de salidas.

Si se trata de un sistema de tiempo continuo, los retardos de salida se deben especificar en las unidades de tiempo dadas por la propiedad TimeUnit. Si se trata de un sistema de tiempo discreto, los retardos de salida se deben especificar como múltiplos enteros del tiempo de muestreo, Ts.

Para más información, consulte Retardos de tiempo en sistemas lineales.

Ts — Tiempo de muestreo

0 (predeterminado) | escalar positivo | -1

Tiempo de muestreo, especificado como:

• 0 si se trata de un sistema de tiempo continuo.

• Un escalar positivo que representa el periodo de muestreo de un sistema de tiempo discreto. Ts se debe especificar en las unidades de tiempo dadas por la propiedad TimeUnit.

• -1 si se trata de un sistema de tiempo discreto con un tiempo de muestreo indefinido.

Nota

Cambiar Ts no discretiza ni remuestrea el modelo. Para la conversión entre representaciones de tiempo continuo y de tiempo discreto, use c2d y d2c. Para cambiar el tiempo de muestreo de un sistema de tiempo discreto use d2d.

TimeUnit — Unidades de la variable tiempo

'seconds' (predeterminado) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

Unidades de la variable tiempo, especificadas como una de las siguientes opciones:

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

Cambiar TimeUnit no afecta a otras propiedades, pero sí cambia el comportamiento general del sistema. Use chgTimeUnit para la conversión entre distintas unidades de tiempo sin modificar el comportamiento del sistema.

InputName — Nombres de los canales de entrada

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Nombres de los canales de entrada, especificados como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una sola entrada.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias entradas.

• '', para no especificar un nombre, para cualquier canal de entrada.

Como alternativa, se pueden asignar nombres a las entradas de un modelo de varias entradas mediante la expansión automática de vectores. Por ejemplo, si sys es un modelo de dos entradas, se puede introducir lo siguiente:

sys.InputName = 'controls';

En este caso, el valor se expandirá automáticamente y los nombres de las entradas serán {'controls(1)';'controls(2)'}.

Se puede usar la notación abreviada u para hacer referencia a la propiedad InputName. Por ejemplo, sys.u es equivalente a sys.InputName.

Utilice InputName para:

• Identificar los canales en la visualización y las gráficas del modelo.

• Extraer los subsistemas de un sistema MIMO.

• Especificar puntos de conexión a la hora de interconectar modelos.

InputUnit — Unidades de los canales de entrada

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Unidades de los canales de entrada, especificadas como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una sola entrada.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias entradas.

• '' para no especificar una unidad, para cualquier canal de entrada.

Use InputUnit para especificar las unidades de las señales de entrada. InputUnit no afecta al comportamiento del sistema.

InputGroup — Grupos de canales de entrada

estructura

Grupos de canales de entrada, especificados como una estructura. Use InputGroup para asignar los canales de entrada de un sistema MIMO a grupos y poder referirse a cada uno de los grupos con un nombre. Los nombres de los campos de InputGroup son los nombres de los grupos y los valores de los campos son los canales de entrada de cada grupo. Por ejemplo, puede introducir lo siguiente para crear grupos de entradas llamados controls y noise que incluyan los canales de entrada 1 y 2, y los canales de entrada 3 y 5, respectivamente.

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

Luego, puede usar el siguiente comando para extraer el subsistema de las entradas del grupo controls a todas las salidas.

sys(:,'controls')

De forma predeterminada, InputGroup es una estructura sin campos.

OutputName — Nombres de los canales de salida

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Nombres de los canales de salida, especificados como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una única salida.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias salidas.

• '', para no especificar un nombre, para cualquier canal de salida.

Como alternativa, se pueden asignar nombres a las salidas de un modelo de varias salidas mediante la expansión automática de vectores. Por ejemplo, si sys es un modelo de dos salidas, se puede introducir lo siguiente:

sys.OutputName = 'measurements';

En este caso, el valor se expandirá automáticamente y los nombres de las salidas serán {'measurements(1)';'measurements(2)'}.

También se puede usar la notación abreviada y para hacer referencia a la propiedad OutputName. Por ejemplo, sys.y es equivalente a sys.OutputName.

Utilice OutputName para:

• Identificar los canales en la visualización y las gráficas del modelo.

• Extraer los subsistemas de un sistema MIMO.

• Especificar puntos de conexión a la hora de interconectar modelos.

OutputUnit — Unidades de los canales de salida

'' (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Unidades los canales de salida, especificadas como una de las siguientes opciones:

• Un vector de caracteres, para un modelo con una única salida.

• Un arreglo de celdas de vectores de caracteres, para un modelo con varias salidas.

• '' para no especificar una unidad, para cualquier canal de salida.

Use OutputUnit para especificar las unidades de las señales de salida. OutputUnit no afecta al comportamiento del sistema.

OutputGroup — Grupos de canales de salida

estructura

Grupos de canales de salida, especificados como una estructura. Use OutputGroup para asignar los canales de salida de un sistema MIMO a grupos y poder referirse a cada uno de los grupos con un nombre. Los nombres de los campos de OutputGroup son los nombres de los grupos y los valores de los campos son los canales de salida de cada grupo. Por ejemplo, puede crear grupos de salidas llamados temperature y measurement que incluyan el canal de salida 1, 3 y los canales de salida 5, respectivamente.

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

Luego, puede usar el siguiente comando para extraer el subsistema de todas las entradas a las salidas del grupo measurement.

sys('measurement',:)

De forma predeterminada, OutputGroup es una estructura sin campos.

Name — Nombre del sistema

'' (predeterminado) | vector de caracteres

Nombre del sistema, especificado como un vector de caracteres. Por ejemplo, 'system_1'.

Notes — Texto especificado por el usuario

{} (predeterminado) | vector de caracteres | arreglo de celdas de vectores de caracteres

Texto especificado por el usuario que desee asociar con el sistema, especificado como un vector de caracteres, o bien un arreglo de celdas de vectores de caracteres. Por ejemplo, 'System is MIMO'.

UserData — Datos especificados por el usuario

[] (predeterminado) | cualquier tipo de dato de MATLAB^®

Datos especificados por el usuario que desee asociar con el sistema, especificado como cualquier tipo de dato de MATLAB.

SamplingGrid — Cuadrícula de muestreo para arreglos de modelos

arreglo de estructuras

Cuadrícula de muestreo para arreglos de modelos, especificada como un arreglo de estructuras.

Use SamplingGrid para hacer un seguimiento de los valores de las variables asociados con cada uno de los modelos de un arreglo de modelos, incluyendo arreglos de modelos identificados lineales invariantes en el tiempo (IDLTI).

Establezca los nombres de los campos de la estructura como nombres de las variables de muestreo. Establezca los valores de los campos como valores de las variables muestreadas asociadas con cada modelo del arreglo. Todas las variables de muestreo deben ser escalares numéricos y todos los arreglos de valores muestreados deben coincidir con las dimensiones del arreglo de modelos.

Por ejemplo, puede crear un arreglo de modelos lineales de 11 por 1, sysarr, tomando instantáneas de un sistema lineal variante en el tiempo en la unidad de tiempo t = 0:10. El siguiente código almacena las muestras de tiempo junto con los modelos lineales.

 sysarr.SamplingGrid = struct('time',0:10)

Del mismo modo, puede crear un arreglo de modelos de 6 por 9, M, muestreando de forma independiente dos variables, zeta y w. El siguiente código mapea los valores de (zeta,w) a M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

Cuando se visualiza M, cada elemento del arreglo incluye los correspondientes valores zeta y w.

M

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

En el caso de los arreglos de modelos obtenidos por linealización de un modelo de Simulink^® para distintos valores de los parámetros o distintos puntos de funcionamiento, el software rellena SamplingGrid automáticamente con los valores de las variables correspondientes a cada elemento del arreglo. Por ejemplo, los comandos de Simulink Control Design™ linearize (Simulink Control Design) y slLinearizer (Simulink Control Design) rellenan SamplingGrid automáticamente.

De forma predeterminada, SamplingGrid es una estructura sin campos.

Funciones del objeto

Las siguientes listas contienen una muestra representativa de las funciones que se pueden usar con los modelos del tipo zpk. En general, cualquier función que se pueda aplicar a modelos de sistemas dinámicos se puede aplicar a un objeto del tipo zpk.

Análisis lineales

step	Respuesta al escalón de un sistema dinámico
impulse	Gráfica de la respuesta al impulso del sistema dinámico; datos de la respuesta al impulso
lsim	Calcular datos de simulación de respuesta en el tiempo de un sistema dinámico para entradas arbitrarias
bode	Respuesta en frecuencia de Bode de un sistema dinámico
nyquist	Respuesta de Nyquist de un sistema dinámico
nichols	Respuesta de Nichols de un sistema dinámico
bandwidth	Ancho de banda de respuestas en frecuencia

Análisis de estabilidad

pole	Polos del sistema dinámico
zero	Ceros y ganancia del sistema dinámico SISO
pzplot	Representar un mapa de polos y ceros del sistema dinámico
margin	Margen de ganancia, margen de fase y frecuencias de cruce

Transformación de modelos

tf	Modelo de función de transferencia
ss	Modelo en espacio de estados
c2d	Conversión de modelos de tiempo continuo a discreto
d2c	Convertir modelos en tiempo discreto a tiempo continuo
d2d	Remuestreo de modelos de tiempo discreto

Interconexión de modelos

feedback	Conexión de feedback de múltiples modelos
connect	Interconexiones del diagrama de bloques de sistemas dinámicos
series	Conexión en serie de dos modelos
parallel	Conexión paralela de dos modelos

Diseño de controladores

pidtune	Algoritmo de ajuste de PID para un modelo de planta lineal
rlocus	Lugar de las raíces de un sistema dinámico
lqr	Diseño de un regulador lineal cuadrático (LQR)
lqg	Diseño lineal cuadrático gaussiano (LQG)
lqi	Control lineal cuadrático integral
kalman	Diseñar un filtro de Kalman para la estimación de estados

Ejemplos

Modelo de cero-polo-ganancia SISO de tiempo continuo

Para este ejemplo, considere el siguiente modelo de cero-polo-ganancia SISO de tiempo continuo:

$$sys(s)=\frac{-2s}{(s-1-i)(s-1+i)(s-2)}$$

Especifique los ceros, los polos y la ganancia, y cree el modelo de cero-polo-ganancia SISO.

zeros = 0;
poles = [1-1i 1+1i 2];
gain = -2;
sys = zpk(zeros,poles,gain)

sys =
 
          -2 s
  --------------------
  (s-2) (s^2 - 2s + 2)
 
Continuous-time zero/pole/gain model.
Model Properties

Modelo de cero-polo-ganancia SISO de tiempo discreto

Para este ejemplo, considere el siguiente modelo de cero-polo-ganancia SISO de tiempo discreto con tiempo de muestreo de 0,1 s:

$$sys(s)=\frac{7(z-1)(z-2)(z-3)}{(z-6)(z-5)(z-4)}$$

Especifique los ceros, los polos, la ganancia y el tiempo de muestreo, y cree el modelo de cero-polo-ganancia SISO de tiempo discreto.

zeros = [1 2 3];
poles = [6 5 4];
gain = 7;
ts = 0.1;
sys = zpk(zeros,poles,gain,ts)

sys =
 
  7 (z-1) (z-2) (z-3)
  -------------------
   (z-6) (z-5) (z-4)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
Model Properties

Concatenar modelos de cero-polo-ganancia SISO en un modelo de cero-polo-ganancia MIMO

Para este ejemplo, cree un modelo de cero-polo-ganancia MIMO concatenando modelos de cero-polo-ganancia SISO. Considere el siguiente modelo de cero-polo-ganancia de tiempo continuo de una entrada y dos salidas:

$$sys(s)=\left[\begin{array}{c}\frac{(s-1)}{(s+1)}\\ \frac{(s+2)}{(s+2+i)(s+2-i)}\end{array}\right].$$

Especifique el modelo de cero-polo-ganancia MIMO concatenando las entradas SISO.

zeros1 = 1;
poles1 = -1;
gain = 1;
sys1 = zpk(zeros1,poles1,gain)

sys1 =
 
  (s-1)
  -----
  (s+1)
 
Continuous-time zero/pole/gain model.
Model Properties

zeros2 = -2;
poles2 = [-2+1i -2-1i];
sys2 = zpk(zeros2,poles2,gain)

sys2 =
 
      (s+2)
  --------------
  (s^2 + 4s + 5)
 
Continuous-time zero/pole/gain model.
Model Properties

sys = [sys1;sys2]

sys =
 
  From input to output...
       (s-1)
   1:  -----
       (s+1)
 
           (s+2)
   2:  --------------
       (s^2 + 4s + 5)
 
Continuous-time zero/pole/gain model.
Model Properties

Modelo de cero-polo-ganancia MIMO de tiempo discreto

Cree un modelo de cero-polo-ganancia para el modelo de tiempo discreto con varias entradas y varias salidas:

$$sys\left(z\right)=\left[\begin{array}{cc}\frac{1}{(z+0.3)}& \frac{z}{(z+0.3)}\\ \frac{-(z-2)}{(z+0.3)}& \frac{3}{(z+0.3)}\end{array}\right]$$

con tiempo de muestreo de ts = 0.2 segundos.

Especifique los ceros y los polos como arreglos de celdas y la ganancia como un arreglo.

zeros = {[] 0;2 []};
poles = {-0.3 -0.3;-0.3 -0.3};
gain = [1 1;-1 3];
ts = 0.2;

Cree el modelo de cero-polo-ganancia MIMO de tiempo discreto.

sys = zpk(zeros,poles,gain,ts)

sys =
 
  From input 1 to output...
          1
   1:  -------
       (z+0.3)
 
       - (z-2)
   2:  -------
       (z+0.3)
 
  From input 2 to output...
          z
   1:  -------
       (z+0.3)
 
          3
   2:  -------
       (z+0.3)
 
Sample time: 0.2 seconds
Discrete-time zero/pole/gain model.
Model Properties

Especificar nombres de entradas para un modelo de cero-polo-ganancia

Especifique los ceros, los polos y la ganancia junto con el tiempo de muestreo y cree el modelo de cero-polo-ganancia especificando los nombres de estados y entradas mediante pares nombre-valor.

zeros = 4;
poles = [-1+2i -1-2i];
gain = 3;
ts = 0.05;
sys = zpk(zeros,poles,gain,ts,'InputName','Force')

sys =
 
  From input "Force" to output:
     3 (z-4)
  --------------
  (z^2 + 2z + 5)
 
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Model Properties

El número de nombres de entradas debe ser congruente con el número de ceros.

Poner nombre a las entradas y salidas puede resultar útil cuando se trate de gráficas de respuesta para sistemas MIMO.

step(sys)

Observe el nombre de entrada Force en el título de la gráfica de respuesta al escalón.

Modelo de cero-polo-ganancia de tiempo continuo a partir de expresión racional

Para este ejemplo, cree un modelo de cero-polo-ganancia de tiempo continuo usando expresiones racionales. A veces, usar una expresión racional es más fácil e intuitivo que especificar los polos y ceros.

Considere el siguiente sistema:

$$sys(s)=\frac{s}{s^2+2s+10}.$$

Para crear el modelo de función de transferencia, primero especifique s como un objeto zpk.

s = zpk('s')

s =
 
  s
 
Continuous-time zero/pole/gain model.
Model Properties

Cree el modelo de cero-polo-ganancia usando s en la expresión racional.

sys = s/(s^2 + 2*s + 10)

sys =
 
         s
  ---------------
  (s^2 + 2s + 10)
 
Continuous-time zero/pole/gain model.
Model Properties

Modelo de cero-polo-ganancia de tiempo discreto a partir de expresión racional

Para este ejemplo, cree un modelo de cero-polo-ganancia de tiempo discreto usando una expresión racional. A veces, usar una expresión racional es más fácil e intuitivo que especificar los polos y ceros.

Considere el siguiente sistema:

$$sys(z)=\frac{z-1}{z^2-1.85z+0.9}.$$

Para crear el modelo de cero-polo-ganancia, primero especifique z como un objeto zpk y el tiempo de muestreo ts.

ts = 0.1;
z = zpk('z',ts)

z =
 
  z
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
Model Properties

Cree el modelo de cero-polo-ganancia usando z en la expresión racional.

sys = (z - 1) / (z^2 - 1.85*z + 0.9)

sys =
 
         (z-1)
  -------------------
  (z^2 - 1.85z + 0.9)
 
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
Model Properties

Modelo de cero-polo-ganancia con propiedades heredadas

Para este ejemplo, cree un modelo de cero-polo-ganancia con propiedades heredadas de otro modelo de cero-polo-ganancia. Considere los siguientes dos modelos de cero-polo-ganancia:

$$sys1(s)=\frac{2s}{s(s+8)}andsys2(s)=\frac{0.8(s-1)}{(s+3)(s-5)}.$$

Para este ejemplo, cree un modelo sys1 con las propiedades TimeUnit y InputDelay definidas en 'minutes'.

zero1 = 0;
pole1 = [0;-8];
gain1 = 2;
sys1 = zpk(zero1,pole1,gain1,'TimeUnit','minutes','InputUnit','minutes')

sys1 =
 
    2 s
  -------
  s (s+8)
 
Continuous-time zero/pole/gain model.
Model Properties

propValues1 = [sys1.TimeUnit,sys1.InputUnit]

propValues1 = 1×2 cell
    {'minutes'}    {'minutes'}

Cree el segundo modelo de cero-polo-ganancia con propiedades heredadas de sys1.

zero = 1;
pole = [-3,5];
gain2 = 0.8;
sys2 = zpk(zero,pole,gain2,sys1)

sys2 =
 
   0.8 (s-1)
  -----------
  (s+3) (s-5)
 
Continuous-time zero/pole/gain model.
Model Properties

propValues2 = [sys2.TimeUnit,sys2.InputUnit]

propValues2 = 1×2 cell
    {'minutes'}    {'minutes'}

Observe que el modelo de cero-polo-ganancia sys2 tiene las mismas propiedades que sys1.

Modelo de cero-polo-ganancia MIMO de ganancia estática

Considere la siguiente matriz de ganancia estática de dos entradas y dos salidas, m:

$$m=\left[\begin{array}{cc}2& 4\\ 3& 5\end{array}\right]$$

Especifique la matriz de ganancia y cree el modelo de cero-polo-ganancia de ganancia estática.

m = [2,4;...
    3,5];
sys1 = zpk(m)

sys1 =
 
  From input 1 to output...
   1:  2
 
   2:  3
 
  From input 2 to output...
   1:  4
 
   2:  5
 
Static gain.
Model Properties

Puede usar el modelo de cero-polo-ganancia de ganancia estática sys1 obtenido arriba y organizarlo en cascada con otro modelo de cero-polo-ganancia.

sys2 = zpk(0,[-1 7],1)

sys2 =
 
       s
  -----------
  (s+1) (s-7)
 
Continuous-time zero/pole/gain model.
Model Properties

sys = series(sys1,sys2)

sys =
 
  From input 1 to output...
           2 s
   1:  -----------
       (s+1) (s-7)
 
           3 s
   2:  -----------
       (s+1) (s-7)
 
  From input 2 to output...
           4 s
   1:  -----------
       (s+1) (s-7)
 
           5 s
   2:  -----------
       (s+1) (s-7)
 
Continuous-time zero/pole/gain model.
Model Properties

Convertir un modelo de espacio de estados en un modelo de cero-polo-ganancia

Para este ejemplo, calcule el modelo de cero-polo-ganancia del siguiente modelo de espacio de estados:

$$A=\left[\begin{array}{cc}-2& -1\\ 1& -2\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ 2& -1\end{array}\right],C=\left[\begin{array}{cc}1& 0\end{array}\right],D=[\begin{array}{cc}0& 1\end{array}].$$

Cree el modelo de espacio de estados usando las matrices de espacio de estados.

A = [-2 -1;1 -2];
B = [1 1;2 -1];
C = [1 0];
D = [0 1];
ltiSys = ss(A,B,C,D);

Convierta el modelo de espacio de estados ltiSys en un modelo de cero-polo-ganancia.

sys = zpk(ltiSys)

sys =
 
  From input 1 to output:
        s
  --------------
  (s^2 + 4s + 5)
 
  From input 2 to output:
  (s^2 + 5s + 8)
  --------------
  (s^2 + 4s + 5)
 
Continuous-time zero/pole/gain model.
Model Properties

Arreglo de modelos de cero-polo-ganancia

Puede usar un lazo for para especificar un arreglo de modelos de cero-polo-ganancia.

En primer lugar, predefina el arreglo de modelos de cero-polo-ganancia con ceros.

sys = zpk(zeros(1,1,3));

Los primeros dos índices representan el número de salidas y entradas de los modelos, en tanto que el tercer índice representa el número de modelos en el arreglo.

Cree el arreglo de modelos de cero-polo-ganancia usando una expresión racional en el lazo for.

s = zpk('s');                                                  
for k = 1:3                                                             
    sys(:,:,k) = k/(s^2+s+k);                                          
end
sys

sys(:,:,1,1) =
 
        1
  -------------
  (s^2 + s + 1)
 

sys(:,:,2,1) =
 
        2
  -------------
  (s^2 + s + 2)
 

sys(:,:,3,1) =
 
        3
  -------------
  (s^2 + s + 3)
 
3x1 array of continuous-time zero/pole/gain models.
Model Properties

Extraer modelos de cero-polo-ganancia de un modelo identificado

Para este ejemplo, extraiga los componentes medidos y de ruido de un modelo polinomial identificado en dos modelos de cero-polo-ganancia independientes.

Cargue el modelo polinomial Box-Jenkins ltiSys en identifiedModel.mat.

load('identifiedModel.mat','ltiSys');

ltiSys es un modelo identificado de tiempo discreto con el formato: $$y(t)=\frac{B}{F}u(t)+\frac{C}{D}e(t)$$, donde $$\frac{B}{F}$$ representa el componente medido y $$\frac{C}{D}$$, el componente de ruido.

Extraiga los componentes medidos y de ruido como modelos de cero-polo-ganancia.

sysMeas = zpk(ltiSys,'measured') 

sysMeas =
 
  From input "u1" to output "y1":
            -0.14256 z^-1 (1-1.374z^-1)
  z^(-2) * -----------------------------
           (1-0.8789z^-1) (1-0.6958z^-1)
 
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties

sysNoise = zpk(ltiSys,'noise')

sysNoise =
 
  From input "v@y1" to output "y1":
            0.045563 (1+0.7245z^-1)
  --------------------------------------------
  (1-0.9658z^-1) (1 - 0.0602z^-1 + 0.2018z^-2)
 
Input groups:        
    Name     Channels
    Noise       1    
                     
Sample time: 0.04 seconds
Discrete-time zero/pole/gain model.
Model Properties

El componente medido puede servir como modelo de planta, mientras que el componente de ruido puede usarse como modelo de perturbaciones para el diseño de un sistema de control.

Modelo de cero-polo-ganancia con retardo de entrada y de salida

Para este ejemplo, cree un modelo de cero-polo-ganancia SISO con un retardo de entrada de 0.5 segundos y un retardo de salida de 2.5 segundos.

zeros = 5;
poles = [7+1i 7-1i -3];
gains = 1;
sys = zpk(zeros,poles,gains,'InputDelay',0.5,'OutputDelay',2.5)

sys =
 
                      (s-5)
  exp(-3*s) * ----------------------
              (s+3) (s^2 - 14s + 50)
 
Continuous-time zero/pole/gain model.
Model Properties

También puede utilizar el comando get para mostrar todas las propiedades de un objeto de MATLAB.

get(sys)

                Z: {[5]}
                P: {[3×1 double]}
                K: 1
    DisplayFormat: 'roots'
         Variable: 's'
          IODelay: 0
       InputDelay: 0.5000
      OutputDelay: 2.5000
        InputName: {''}
        InputUnit: {''}
       InputGroup: [1×1 struct]
       OutputName: {''}
       OutputUnit: {''}
      OutputGroup: [1×1 struct]
            Notes: [0×1 string]
         UserData: []
             Name: ''
               Ts: 0
         TimeUnit: 'seconds'
     SamplingGrid: [1×1 struct]

Para más información sobre cómo especificar el retardo de tiempo para un modelo LTI, consulte Especificar retardos de tiempo.

Diseño de control utilizando modelos de cero-polo-ganancia

Para este ejemplo, diseñe un controlador PID de 2-DOF con un ancho de banda objetivo de 0.75 rad/s para un sistema representado por el siguiente modelo de cero-polo-ganancia:

$$sys(s)=\frac{1}{s^2+0.5s+0.1}$$

Cree un objeto de modelo de cero-polo-ganancia sys utilizando el comando zpk.

zeros = [];
poles = [-0.25+0.2i;-0.25-0.2i];
gain = 1;
sys = zpk(zeros,poles,gain)

sys =
 
            1
  ---------------------
  (s^2 + 0.5s + 0.1025)
 
Continuous-time zero/pole/gain model.
Model Properties

Utilizando el ancho de banda objetivo, use pidtune para generar un controlador de 2-DOF.

wc = 0.75;
C2 = pidtune(sys,'PID2',wc)

C2 =
 
                       1              
  u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
                       s              

  with Kp = 0.512, Ki = 0.0975, Kd = 0.574, b = 0.38, c = 0
 
Continuous-time 2-DOF PID controller in parallel form.
Model Properties

Utilizar el tipo 'PID2', pidtune genera un controlador de 2-DOF, representado como un objeto pid2. La ventana confirma este resultado. La ventana también muestra que pidtune ajusta todos los coeficientes del controlador, incluyendo las pesos de valores de consigna b y c, para equilibrar el rendimiento y la robustez.

Para un ajuste interactivo del PID en Live Editor, consulte la tarea Tune PID Controller de Live Editor. Esta tarea permite diseñar un controlador PID de forma interactiva y genera automáticamente código de MATLAB para un script en vivo.

Para un ajuste interactivo del PID en una app independiente, utilice PID Tuner. Consulte Diseño de controladores PID para el seguimiento rápido de referencia para ver un ejemplo de cómo diseñar un controlador con la app.

Calcular la aproximación de ZPK truncada del modelo disperso

Desde R2025a

Este ejemplo muestra cómo obtener el modelo de cero-polo-ganancia truncado de un modelo disperso de espacio de estados. Este ejemplo utiliza un modelo disperso obtenido linealizando un modelo térmico de distribución de calor en una barra cilíndrica.

Cargue los datos del modelo.

load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)

Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.

Analice la respuesta en frecuencia del modelo.

sigmaplot(sys,w)

Para obtener una aproximación truncada, utilice zpk y especifique la banda de frecuencia de enfoque. Para este modelo, puede utilizar un rango de frecuencia de 0 rad/s a 0,01 rad/s para obtener la aproximación de orden inferior.

zsys = zpk(sys,Focus=[0 1e-2],Display="off");

Compare la respuesta en frecuencia.

sigmaplot(sys,zsys,w)

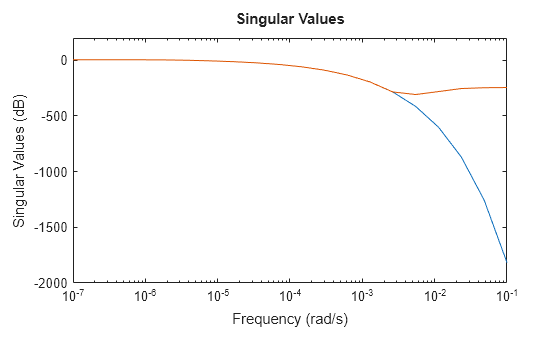
Este modelo térmico tiene una atenuación muy pronunciada más allá de 0,001 rad/s. De forma predeterminada, el modelo reducido obtenido usando zpk no proporciona una buena coincidencia para esta atenuación. Para mitigar esto, puede utilizar el argumento RollOff de zpk y especificar un valor de atenuación mínimo más allá de la banda de frecuencia de enfoque. Especifique un valor de pendiente de atenuación de -45, que corresponde a una tasa de al menos –900 db/década.

zsys2 = zpk(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,zsys2,w)

El modelo reducido ahora proporciona una aproximación mucho mejor del valor de atenuación. Sin embargo, en este ejemplo, reajustar la pendiente de atenuación usando zpk requiere volver a calcular ceros y polos. Esto puede demandar una alta carga computacional en el caso de modelos a gran escala. Como alternativa, puede utilizar el método de truncamiento de polos y ceros de reducespec y ajustar la atenuación sin coste de cálculo adicional, después de que el software haya calculado los polos y ceros. Para ver un ejemplo, consulte Zero-Pole Truncation of Thermal Model.

Algoritmos

zpk utiliza la función roots de MATLAB para convertir funciones de transferencia, y las funciones zero y pole para convertir modelos de espacio de estados.

Para convertir modelos dispersos, zpk utiliza el algoritmo de Krylov--Schur [1] para iteraciones de potencia inversa a fin de calcular polos y ceros en la banda de frecuencia especificada.

Referencias

[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.

Historial de versiones

Introducido antes de R2006a

R2025a: Calcular la aproximación de cero-polo-ganancia truncada de modelos dispersos

Ahora puede utilizar zpk para convertir modelos de espacio de estados dispersos y obtener una aproximación de cero-polo-ganancia truncada. zpk calcula un subconjunto de los ceros y polos de los modelos dispersos, normalmente en una banda de frecuencia baja específica [0 f_max]. Esto puede producir mejores aproximaciones de frecuencia baja que la reducción del orden del modelo por truncamiento modal, a expensas de más cálculos. zpk también proporciona control directo sobre la pendiente de atenuación más allá de la frecuencia f_max. Utilice la nueva sintaxis zsys = zpk(sparseSys,Name=Value) para obtener una aproximación basada en opciones específicas, como el rango de frecuencia del foco. Para ver un ejemplo, consulte Calcular la aproximación de ZPK truncada del modelo disperso.

Consulte también

filt | frd | get | set | ss | zpkdata | genss | tf | realp | genmat

Temas

• Funciones de transferencia
• What Are Model Objects?
• Modelos numéricos de tiempo discreto
• Using the Right Model Representation
• Uso de FEEDBACK para cerrar lazos de feedback