Transformada de Fourier

La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Definición de transformada de Fourier

La transformada de Fourier es una representación de una imagen como una suma de exponenciales complejas de magnitudes, frecuencias y fases variables. La transformada de Fourier tiene un papel esencial en una amplia gama de aplicaciones de procesamiento de imágenes, como la mejora, el análisis, la restauración y la compresión.

Si f(m,n) es una función de dos variables espaciales discretas m y n, la transformada de Fourier bidimensional de f(m,n) se define por la relación

$F (ω_{1}, ω_{2}) = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} f (m, n) e^{- j ω_{1} m} e^{- j ω_{2} n} .$

Las variables ω₁ y ω₂ son variables de frecuencia; sus unidades son radianes por muestra. F(ω₁,ω₂) se suele denominar representación de dominio de frecuencia de f(m,n). F(ω₁,ω₂) es una función de valores complejos que es periódica tanto en ω₁ como en ω₂, con periodo $2 π$ . Debido a la periodicidad, normalmente solo se muestra el intervalo $- π \leq ω_{1}, ω_{2} \leq π$ . Tenga en cuenta que F(0,0) es la suma de todos los valores de f(m,n). Por este motivo, F(0,0) se suele denominar componente constante o componente de DC de la transformada de Fourier. (DC significa corriente continua; se trata de un término perteneciente a la ingeniería eléctrica que hace referencia a una fuente de alimentación de voltaje constante, al contrario que una fuente de alimentación cuyo voltaje varía sinusoidalmente).

La inversa de una transformada es una operación que, cuando se realiza en una imagen transformada, produce la imagen original. La transformada de Fourier inversa bidimensional viene dada por

$f (m, n) = \frac{1}{4 π^{2}} \int_{ω_{1} = - π}^{π} \int_{ω_{2} = - π}^{π} F (ω_{1}, ω_{2}) e^{j ω_{1} m} e^{j ω_{2} n} d ω_{1} d ω_{2} .$

En términos generales, esta ecuación significa que f(m,n) se puede representar como la suma de un número infinito de exponenciales complejas (sinusoides) con diferentes frecuencias. La magnitud y la fase de la contribución en las frecuencias (ω₁,ω₂) vienen dadas por F(ω₁,ω₂).

Visualizar la transformada de Fourier

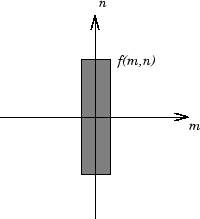
Para ilustrarlo, considere una función f(m,n) igual a 1 dentro de una región rectangular y a 0 en cualquier otra parte. Para simplificar el diagrama, f(m,n) se muestra como función continua, aunque las variables m y n sean discretas.

Función rectangular

Plot of rectangular function f(m,n) in the spatial domain

La figura siguiente muestra, como gráfica de malla, la magnitud de la transformada de Fourier,

$| F (ω_{1}, ω_{2}) |,$

de la función rectangular mostrada en la figura anterior. La gráfica de malla de la magnitud es una forma habitual de visualizar la transformada de Fourier.

Imagen de magnitud de una función rectangular

Mesh plot of the magnitude of the Fourier transform of the rectangular function f(m,n), plotted as a function of the horizontal frequency, ω1, and vertical frequency, ω2

El pico en el centro de la gráfica es F(0,0), que es la suma de todos los valores de f(m,n). La gráfica también muestra que F(ω₁,ω₂) tiene más energía a frecuencias horizontales altas que a frecuencias verticales altas. Esto indica que las secciones transversales horizontales de f(m,n) son pulsos estrechos, mientras que las secciones transversales verticales son pulsos anchos. Los pulsos estrechos tienen más contenido de alta frecuencia que los pulsos anchos.

Otra forma habitual de visualizar la transformada de Fourier es mostrando

$\log | F (ω_{1}, ω_{2}) |$

como imagen, como se muestra.

Logaritmo de la transformada de Fourier de una función rectangular

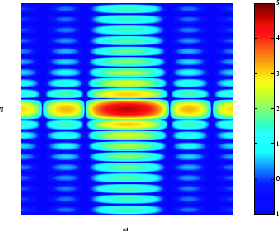
2-D pot of the log of the Fourier transform of the rectangular function f(m,n), plotted as a function of the horizontal frequency, ω1, and vertical frequency, ω2

Usar el logaritmo ayuda a revelar detalles de la transformada de Fourier en regiones en las que F(ω₁,ω₂) está muy cerca de 0.

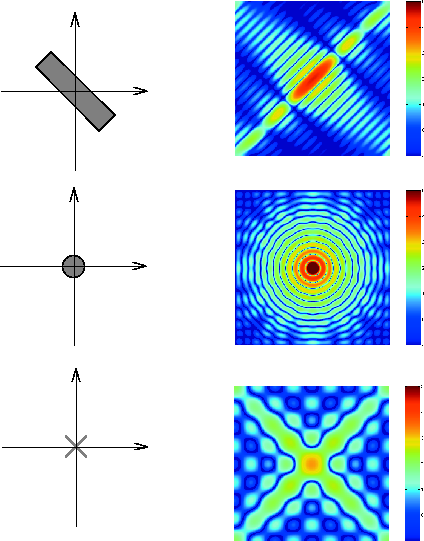
A continuación, se muestran ejemplos de la transformada de Fourier para otras formas simples.

Transformadas de Fourier de algunas formas simples

2-D plots of the Fourier transforms of a rectangle tilted forty-five degrees, a circle centered at (0, 0), and an X shape centered at (0, 0)

Transformada discreta de Fourier

Trabajar con la transformada de Fourier en un ordenador normalmente implica una forma de la transformada conocida como transformada discreta de Fourier (DFT). Una transformada discreta es una transformada cuyos valores de entrada y salida son muestras discretas, por lo que resulta práctica para manipularla en un ordenador. Hay dos motivos principales para usar esta forma de la transformada:

La entrada y la salida de la DFT son discretas, por lo que resulta práctica para manipularla en un ordenador.
Existe un algoritmo rápido para calcular la DFT conocido como transformada rápida de Fourier (FFT).

La DFT se define normalmente para una función discreta f(m,n) que es distinta de cero solo sobre la región finita $0 \leq m \leq M - 1$ y $0 \leq n \leq N - 1$ . Las relaciones de DFT bidimensional de M por N y DFT inversa de M por N vienen dadas por

$F (p, q) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} f (m, n) e^{- j 2 π p m / M} e^{- j 2 π q n / N} \begin{matrix} p = 0, 1, ..., M - 1 \\ q = 0, 1, ..., N - 1 \end{matrix}$

$f (m, n) = \frac{1}{M N} \sum_{p = 0}^{M - 1} \sum_{q = 0}^{N - 1} F (p, q) e^{j 2 π p m / M} e^{j 2 π q n / N} \begin{matrix} m = 0, 1, ..., M - 1 \\ n = 0, 1, ..., N - 1 \end{matrix}$

Los valores F(p,q) son los coeficientes DFT de f(m,n). El coeficiente de frecuencia cero, F(0,0), se suele denominar "componente de DC". DC es un término perteneciente a la ingeniería eléctrica que significa corriente continua. (Tenga en cuenta que los índices de las matrices en MATLAB^® siempre comienzan en 1 en lugar de 0; por lo tanto, los elementos de las matrices f(1,1) y F(1,1) corresponden a las cantidades matemáticas f(0,0) y F(0,0), respectivamente).

Las funciones de MATLAB fft, fft2 y fftn aplican el algoritmo de la transformada rápida de Fourier para calcular la DFT unidimensional, la DFT bidimensional y la DFT en N dimensiones, respectivamente. Las funciones ifft, ifft2 y ifftn calculan la DFT inversa.

Relación con la transformada de Fourier

Los coeficientes DFT F(p,q) son muestras de la transformada de Fourier F(ω₁,ω₂).

$\begin{matrix} F (p, q) = F (ω_{1}, ω_{2}) |_{\begin{array}{l} ω_{1} = 2 π p / M \\ ω_{2} = 2 π q / N \end{array}} & \begin{array}{l} p = 0, 1, ..., M - 1 \\ q = 0, 1, ..., N - 1 \end{array} \end{matrix}$

Visualizar la transformada discreta de Fourier

Construya una matriz f que sea similar a la función f(m,n) en el ejemplo de Definición de transformada de Fourier. Recuerde que f(m,n) es igual a 1 dentro de la región rectangular y a 0 en cualquier otra parte. Utilice una imagen binaria para representar f(m,n).
```
f = zeros(30,30);
f(5:24,13:17) = 1;
imshow(f,"InitialMagnification","fit")
```
Calcule y visualice la DFT de 30 por 30 de f con estos comandos.
```
F = fft2(f);
F2 = log(abs(F));
imshow(F2,[-1 5],"InitialMagnification","fit");
colormap(jet); colorbar
```
Transformada discreta de Fourier calculada sin relleno
Esta gráfica difiere de la transformada de Fourier mostrada en Visualizar la transformada de Fourier. Primero, el muestreo de la transformada de Fourier es mucho más grueso. Segundo, el coeficiente de frecuencia cero se muestra en la esquina superior izquierda en lugar de en la ubicación tradicional en el centro.
Para obtener un muestreo más fino de la transformada de Fourier, añada un relleno de ceros a f cuando calcule su DFT. El relleno de ceros y el cálculo de la DFT se pueden realizar en un solo paso con este comando.
```
F = fft2(f,256,256);
```
Este comando rellena f con ceros para que sea de 256 por 256 antes de calcular la DFT.
```
imshow(log(abs(F)),[-1 5]); colormap(jet); colorbar
```
Transformada discreta de Fourier calculada con relleno
Sin embargo, el coeficiente de frecuencia cero se sigue mostrando en la esquina superior izquierda en lugar de en el centro. Puede solucionar este problema usando la función fftshift, que intercambia los cuadrantes de F para que el coeficiente de frecuencia cero esté en el centro.
```
F = fft2(f,256,256);F2 = fftshift(F);
imshow(log(abs(F2)),[-1 5]); colormap(jet); colorbar
```
La gráfica resultante es idéntica a la mostrada en Visualizar la transformada de Fourier.

Aplicaciones de la transformada de Fourier

Esta sección presenta algunas de las muchas aplicaciones relacionadas con el procesamiento de imágenes de la transformada de Fourier.

Respuesta en frecuencia de filtros lineales

La transformada de Fourier de la respuesta al impulso de un filtro lineal proporciona la respuesta en frecuencia del filtro. La función freqz2 calcula y muestra la respuesta en frecuencia de un filtro. La respuesta en frecuencia del núcleo de convolución gaussiano muestra que este filtro pasa frecuencias bajas y atenúa frecuencias altas.

h = fspecial("gaussian");
freqz2(h)

Respuesta en frecuencia de un filtro gaussiano

Mesh plot of the magnitude of the frequency response of a Gaussian filter.

Para más información sobre el filtrado lineal, el diseño de filtros y las respuestas en frecuencia, consulte Design Linear Image Filters in the Frequency Domain.

Realizar una convolución rápida con la transformada de Fourier

Abrir script en vivo

En este ejemplo se muestra cómo llevar a cabo la convolución rápida de dos matrices con la transformada de Fourier. Una de las propiedades clave de la transformada de Fourier es que la multiplicación de dos transformadas de Fourier se corresponde con la convolución de las funciones espaciales asociadas. Esta propiedad, junto con la transformada rápida de Fourier, es la base para un algoritmo de convolución rápido.

Nota: El método de convolución basado en FFT se usa con mayor frecuencia para entradas grandes. Para entradas pequeñas, suele ser más rápido usar la función imfilter.

Cree dos matrices simples, A y B. A es una matriz de M por N y B es una matriz de P por Q.

A = magic(3);
B = ones(3);

Rellene A y B con ceros para que sean al menos de (M+P-1) por (N+Q-1). (A menudo, A y B se rellenan con ceros hasta un tamaño que es una potencia de 2 porque fft2 es más rápido para estos tamaños). El ejemplo rellena las matrices para que sean de 8 por 8.

A(8,8) = 0;
B(8,8) = 0;

Calcule la DFT bidimensional de A y B con la función fft2. Multiplique las dos DFT juntas y calcule la DFT bidimensional inversa del resultado con la función ifft2.

C = ifft2(fft2(A).*fft2(B));

Extraiga la parte distinta de cero del resultado y elimine la parte imaginaria provocada por el error de redondeo.

C = C(1:5,1:5);
C = real(C)

C = 5×5

    8.0000    9.0000   15.0000    7.0000    6.0000
   11.0000   17.0000   30.0000   19.0000   13.0000
   15.0000   30.0000   45.0000   30.0000   15.0000
    7.0000   21.0000   30.0000   23.0000    9.0000
    4.0000   13.0000   15.0000   11.0000    2.0000

Realizar una correlación basada en FFT para localizar características de una imagen

Abrir script en vivo

En este ejemplo se muestra cómo usar la transformada de Fourier para realizar una correlación, que está estrechamente relacionada con la convolución. La correlación se puede utilizar para localizar características dentro de una imagen. En este contexto, la correlación se suele denominar correspondencia de plantillas.

Lea una imagen de muestra en el área de trabajo.

bw = imread('text.png');

Cree una plantilla para realizar la correspondencia extrayendo la letra "a" de la imagen. Tenga en cuenta que también puede crear la plantilla usando la sintaxis interactiva de la función imcrop.

a = bw(32:45,88:98);

Calcule la correlación de la imagen de plantilla con la imagen original rotando la imagen de plantilla 180 grados y, después, usando la técnica de convolución basada en FFT. (La convolución equivale a la correlación si rota el núcleo de convolución 180 grados). Para realizar la correspondencia entre la plantilla y la imagen, use las funciones fft2 y ifft2. En la imagen resultante, los picos más brillantes se corresponden con las veces que aparece la letra.

C = real(ifft2(fft2(bw) .* fft2(rot90(a,2),256,256)));
figure
imshow(C,[]) % Scale image to appropriate display range.

Figure contains an axes object. The hidden axes object contains an object of type image.

Para ver las ubicaciones de la plantilla en la imagen, busque el valor máximo de píxel y, después, defina un valor umbral menor que este máximo. La imagen umbralizada muestra las ubicaciones de estos picos como puntos blancos en la imagen umbralizada de correlación. (Para ver las ubicaciones más fácilmente en esta figura, el ejemplo dilata la imagen umbralizada para ampliar el tamaño de los puntos).

max(C(:))

ans = 
68

thresh = 60; % Use a threshold that's a little less than max.
D = C > thresh;
se = strel('disk',5);
E = imdilate(D,se);
figure
imshow(E) % Display pixels with values over the threshold.

Figure contains an axes object. The hidden axes object contains an object of type image.

Consulte también

fft2 | ifft2 | freqz2

Temas

Design Linear Image Filters in the Frequency Domain