La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

optimproblem

Crear un problema de optimización

Sintaxis

prob = optimproblem

prob = optimproblem(Name,Value)

Descripción

Utilice optimproblem para crear un problema de optimización.

Sugerencia

Para ver el flujo de trabajo completo, consulte Flujo de trabajo de optimización basada en problemas.

prob = optimproblem crea un problema de optimización con propiedades predeterminadas.

prob = optimproblem(Name,Value) utiliza opciones adicionales especificadas por uno o más argumentos de par Name,Value. Por ejemplo, para especificar un problema de maximización en lugar de un problema de minimización, utilice prob = optimproblem('ObjectiveSense','maximize').

Nota

Todos los nombres en un problema de optimización deben ser únicos. Específicamente, todos los nombres de variables, de funciones objetivo y de funciones de restricción deben ser diferentes.

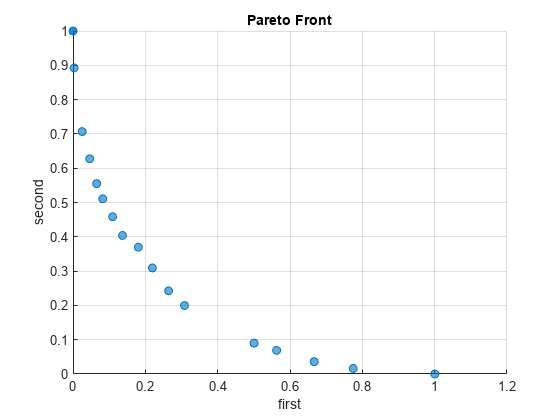
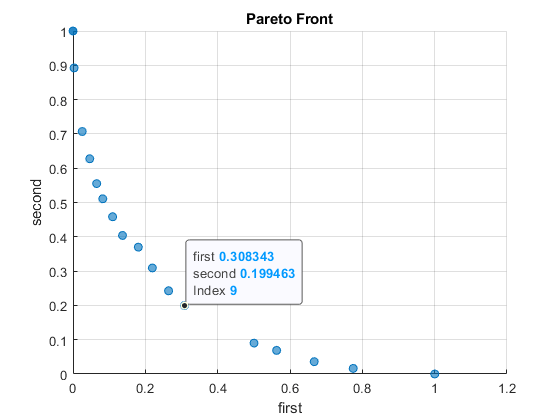
Ejemplos

Crear un problema de optimización

Cree un problema de optimización con propiedades predeterminadas.

prob = optimproblem

prob = 
  OptimizationProblem with properties:

       Description: ''
    ObjectiveSense: 'minimize'
         Variables: [0x0 struct] containing 0 OptimizationVariables
         Objective: [0x0 OptimizationExpression]
       Constraints: [0x0 struct] containing 0 OptimizationConstraints

  No problem defined.

Crear y resolver un problema de maximización

Cree un problema de programación lineal para su maximización. El problema tiene dos variables positivas y tres restricciones de desigualdad lineales.

prob = optimproblem('ObjectiveSense','max');

Cree variables positivas. Incluya una función objetivo en el problema.

x = optimvar('x',2,1,'LowerBound',0);
prob.Objective = x(1) + 2*x(2);

Cree restricciones de desigualdad lineales en el problema.

cons1 = x(1) + 5*x(2) <= 100;
cons2 = x(1) + x(2) <= 40;
cons3 = 2*x(1) + x(2)/2 <= 60;
prob.Constraints.cons1 = cons1;
prob.Constraints.cons2 = cons2;
prob.Constraints.cons3 = cons3;

Revise el problema.

show(prob)

  OptimizationProblem : 

	Solve for:
       x

	maximize :
       x(1) + 2*x(2)


	subject to cons1:
       x(1) + 5*x(2) <= 100

	subject to cons2:
       x(1) + x(2) <= 40

	subject to cons3:
       2*x(1) + 0.5*x(2) <= 60

	variable bounds:
       0 <= x(1)
       0 <= x(2)

Resuelva el problema.

sol = solve(prob);

Solving problem using linprog.

Optimal solution found.

sol.x

ans = 2×1

    25
    15

Crear y resolver un problema multiobjetivo

Cree un problema con dos funciones objetivo de una variable x en 2D. Cree las funciones objetivo como expresiones en x y colóquelas en el objetivo como estructuras.

x = optimvar("x",2,LowerBound=-2,UpperBound=2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = norm(x - [1;0])^2;

Resuelva el problema.

rng default % For reproducibility
sol = solve(prob);

Solving problem using gamultiobj.
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

Represente la solución.

paretoplot(sol)

Examine un punto del frente de Pareto. Para hacerlo, haga clic en la figura y en la herramienta Data Tips:

Después haga clic en un punto del frente de Pareto.

El índice del punto mostrado es 9. Puede encontrar el valor x asociado a este punto como la solución con índice 9.

sol(9).x

ans = 2×1

    0.5544
   -0.0306

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value el valor correspondiente. Los argumentos nombre-valor deben aparecer tras otros argumentos, aunque no importa el orden de los pares.

En versiones anteriores a R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.

Ejemplo: Para especificar un problema de maximización, utilice prob = optimproblem('ObjectiveSense','maximize').

Constraints — Restricciones de problema

Arreglo OptimizationConstraint | estructura con arreglos OptimizationConstraint como campos

Restricciones de problema, especificadas como un arreglo OptimizationConstraint o una estructura con arreglos OptimizationConstraint como campos.

Ejemplo: prob = optimproblem('Constraints',sum(x,2) == 1)

Description — Etiqueta de problema

'' (predeterminado) | cadena | vector de caracteres

Etiqueta de problema, especificada como una cadena o vector de caracteres. El software no utiliza Description para el cálculo. Description es una etiqueta arbitraria que puede utilizar por cualquier motivo. Por ejemplo, puede compartir, archivar o presentar un modelo o problema, y almacenar información descriptiva sobre el modelo o el problema en Description.

Ejemplo: "An iterative approach to the Traveling Salesman problem"

Tipos de datos: char | string

Objective — Función objetivo

escalar OptimizationExpression | arreglo de OptimizationExpression | estructura con OptimizationExpression escalar como campos

Función objetivo, especificada como objeto OptimizationExpression escalar, arreglo de objetos OptimizationExpression o estructura con OptimizationExpression escalar como campos.

• En un problema escalar (de objetivo único), especifique la función objetivo como una expresión de optimización escalar o como una estructura con una expresión de optimización escalar como valor.

• En un problema multiobjetivo, especifique las funciones objetivo como una expresión de optimización de valor vectorial, como un arreglo de expresiones de optimización o como una estructura de expresiones de optimización. Por ejemplo, este objetivo es una estructura de expresiones de optimización en una variable de optimización escalar x:

  prob = optimproblem;
  prob.Objective.first = x^2;
  prob.Objective.second = (x + 1)^2;

Ejemplo: prob = optimproblem('Objective',sum(sum(x))) para una variable x en 2D.

Ejemplo: prob = optimproblem('Objective',(x-a).^2) donde x y a tienen un tamaño de 2 por 1, y x es una variable de optimización.

ObjectiveSense — Sentido de optimización

'minimize' (predeterminado) | 'min' | 'maximize' | 'max' | estructura con los valores enumerados como campos

Sentido de optimización, especificado como 'minimize' o 'maximize'. También puede especificar 'min' para obtener 'minimize' o 'max' para obtener 'maximize'. La función solve minimiza un objetivo cuando ObjectiveSense es 'minimize' y maximiza un objetivo cuando ObjectiveSense es 'maximize'.

ObjectiveSense puede ser una estructura con valores 'minimize', 'min', 'maximize' o 'max'. Puede utilizar este formato cuando el objetivo del problema sea una estructura. Las estructuras Objective y ObjectiveSense deben tener los mismos nombres de campo para que ObjectiveSense se aplique al Objective correspondiente. Por ejemplo:

x = optimvar('x',2,"UpperBound",2,"LowerBound",-2);
prob = optimproblem;
prob.Objective.first = norm(x)^2;
prob.Objective.second = -norm(x - [1;0])^2;
prob.ObjectiveSense.first = "min";
prob.ObjectiveSense.second = "max";

Si Objective es una estructura, puede especificar ObjectiveSense como un nombre tipo 'max'. En este caso, todos los objetivos tienen el mismo ObjectiveSense.

Ejemplo: prob = optimproblem('ObjectiveSense','max')

Tipos de datos: char | string

Argumentos de salida

prob — Problema de optimización

Objeto OptimizationProblem

Problema de optimización, devuelto como un objeto OptimizationProblem. Habitualmente, para completar la descripción del problema se especifican una función objetivo y restricciones. No obstante, puede tener un problema de factibilidad, que no tiene función objetivo, o puede tener un problema sin restricciones. Resuelva un problema completo llamando a solve.

Advertencia

El enfoque basado en problemas no es compatible con valores complejos en una función objetivo, igualdades no lineales o desigualdades no lineales. Si el cálculo de una función tiene un valor complejo, incluso como valor intermedio, el resultado final puede ser incorrecto.

Historial de versiones

Introducido en R2017b

Consulte también

optimvar | OptimizationProblem | solve

Temas

• Configuración de optimización basada en problemas
• Flujo de trabajo de optimización basada en problemas