Chi-Square Distribution
Overview
The chi-square (χ2) distribution is a one-parameter family of curves. The chi-square distribution is commonly used in hypothesis testing, particularly the chi-square test for goodness of fit.
Statistics and Machine Learning Toolbox™ offers multiple ways to work with the chi-square distribution.
Use distribution-specific functions (
chi2cdf,chi2inv,chi2pdf,chi2rnd,chi2stat) with specified distribution parameters. The distribution-specific functions can accept parameters of multiple chi-square distributions.Use generic distribution functions (
cdf,icdf,pdf,random) with a specified distribution name ('Chisquare') and parameters.
Parameters
The chi-square distribution uses the following parameter.
| Parameter | Description | Support |
|---|---|---|
| nu (ν) | Degrees of freedom | ν = 1, 2, 3,... |
The degrees of freedom parameter is typically an integer, but chi-square functions accept any positive value.
The sum of two chi-square random variables with degrees of freedom ν1 and ν2 is a chi-square random variable with degrees of freedom ν = ν1 + ν2.
Probability Density Function
The probability density function (pdf) of the chi-square distribution is
where ν is the degrees of freedom and Γ( · ) is the Gamma function.
For an example, see Compute Chi-Square Distribution pdf.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the chi-square distribution is
where ν is the degrees of freedom and Γ( · ) is the Gamma function. The result p is the probability that a single observation from the chi-square distribution with ν degrees of freedom falls in the interval [0, x].
For an example, see Compute Chi-Square Distribution cdf.
Inverse Cumulative Distribution Function
The inverse cumulative distribution function (icdf) of the chi-square distribution is
where
ν is the degrees of freedom, and Γ( · ) is the Gamma function. The result p is the probability that a single observation from the chi-square distribution with ν degrees of freedom falls in the interval [0, x].
Descriptive Statistics
The mean of the chi-square distribution is ν.
The variance of the chi-square distribution is 2ν.
Examples
Compute Chi-Square Distribution pdf
Compute the pdf of a chi-square distribution with 4 degrees of freedom.
x = 0:0.2:15; y = chi2pdf(x,4);
Plot the pdf.
figure; plot(x,y) xlabel('Observation') ylabel('Probability Density')
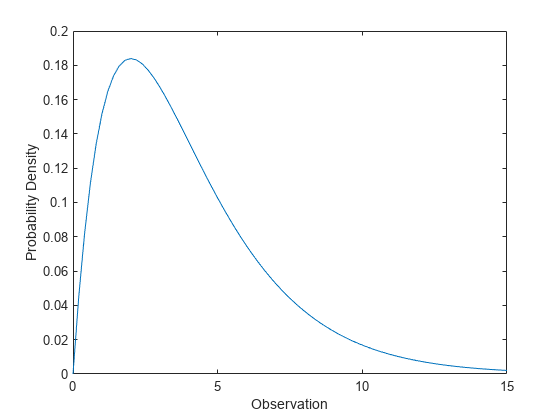
The chi-square distribution is skewed to the right, especially for few degrees of freedom.
Compute Chi-Square Distribution cdf
Compute the cdf of a chi-square distribution with 4 degrees of freedom.
x = 0:0.2:15; y = chi2cdf(x,4);
Plot the cdf.
figure; plot(x,y) xlabel('Observation') ylabel('Cumulative Probability')

Related Distributions
F Distribution — The F distribution is a two-parameter distribution that has parameters ν1 (numerator degrees of freedom) and ν2 (denominator degrees of freedom). The F distribution can be defined as the ratio , where χ21 and χ22 are both independent and chi-square distributed with ν1 and ν2 degrees of freedom, respectively.
Gamma Distribution — The gamma distribution is a two-parameter continuous distribution that has parameters a (shape) and b (scale). The chi-square distribution is equal to the gamma distribution with 2a = ν and b = 2.
Noncentral Chi-Square Distribution — The noncentral chi-square distribution is a two-parameter continuous distribution that has parameters ν (degrees of freedom) and δ (noncentrality). The noncentral chi-square distribution is equal to the chi-square distribution when δ = 0.
Normal Distribution — The normal distribution is a two-parameter continuous distribution that has parameters μ (mean) and σ (standard deviation). The standard normal distribution occurs when μ = 0 and σ = 1.
If Z1, Z2, …, Zn are independent standard normal random variables, then has a chi-square distribution with degrees of freedom ν = n – 1.
If a set of n observations is normally distributed with variance σ2 and sample variance s2, then has a chi-square distribution with degrees of freedom ν = n – 1. This relationship is used to calculate confidence intervals for the estimate of the normal parameter σ2 in the function
normfit.Student's t Distribution — The Student's t distribution is a one-parameter continuous distribution that has parameter ν (degrees of freedom). If Z has a standard normal distribution, χ2 has a chi-square distribution with degrees of freedom ν, and Z and χ2 are independent, then has a Student's t distribution with degrees of freedom ν.
Wishart Distribution — The Wishart distribution is a higher dimensional analog of the chi-square distribution.
References
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.
[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.
See Also
chi2cdf | chi2pdf | chi2inv | chi2stat | chi2gof | chi2rnd