Modelling and Simulation of Radar Signal Processing Applications with MATLAB
From the series: Radar Applications Webinar Series
Overview
Engineers working on signal processing for radar applications simulate systems at varying levels of abstraction and use a combination of methods to express their designs and ideas.
This session looks at how recent developments in MATLAB® and Simulink® enable more effective design and development of radar system models through efficient simulation. Highlights include:
Modelling & Simulation of Radar Systems for Aero Defense applications
- Challenges faced by radar engineers
- Making engineering trade-offs early in the design cycle
- Selecting the right level of model abstraction
- Overview of deploying radar signal processing algorithms to processors & FPGAs
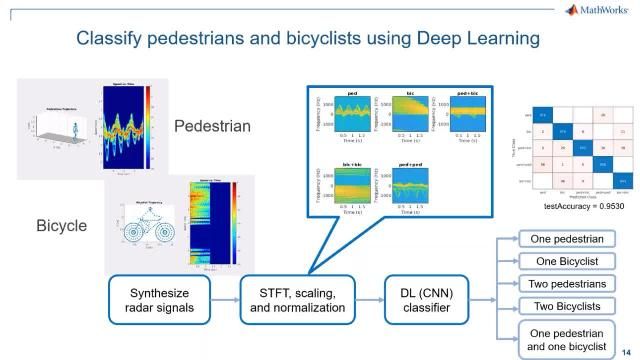
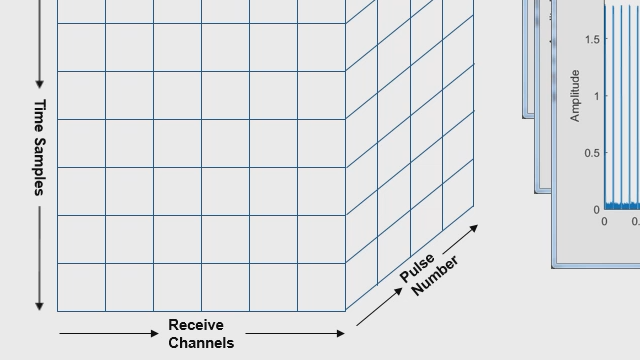
Development of signal processor and extractor module for 3D surveillance radar using MATLAB
- Modelling customized signal processor modules for 3D surveillance radars
- Discussion on algorithmic complexities in conventional approach
- Ease of implementing and testing algorithms in MATLAB
- Quantifying performance during multiple developmental phases
About the Presenter
Sumit Garg | Sr. Application Engineer | MathWorks
Sumit Garg is a senior application engineer at MathWorks India specializing in design analysis and implementation of radar signal processing and data processing applications. He works closely with customers across domains to help them use MATLAB® and Simulink® in their workflows. He has over ten years of industrial experience in the design and development of hardware and software applications in the radar domain. He has been a part of the complete lifecycle of projects pertaining to aerospace and defense applications. Prior to joining MathWorks, he worked for Bharat Electronics Limited (BEL) and Electronics and Radar Development Establishment (LRDE) as a senior engineer. He holds a bachelor’s degree in electronics and telecommunication from Panjab University, Chandigarh.
Mohit Gaur | Manager | Bharat Electronics Limited
Mohit Gaur is working as Deputy Manager in Bharat Electronics Ltd, focusing on development of radar systems for defense applications. His core domain is Radar Signal and Data Processing and Radar system Engineering . Mohit holds a bachelor’s degree in Electronics and Communications from Delhi College of Engineering, India, and currently pursuing M Tech in Microelectronics from IIT Madras. He is actively involved in development of upcoming Radars.
Pratishtha Jaiswal | Sr. Engineer | Bharat Electronics Limited
Pratishtha Jaiswal is working as Senior Engineer in Bharat Electronics Limited, focusing on development of Radar Systems for defence applications. Her core domain is Radar Data Processing. Pratishtha holds a bachelor’s degree in Computer Science And Engineering from Institute Of Engineering And Technology Lucknow, India. She is involved in development and integration of upcoming Radars.
Recorded: 8 Feb 2023