RF Data Analysis and System Design for Scientific Applications, Part 1: Getting Started with RF Data Analysis
From the series: RF Data Analysis and System Design for Scientific Applications
Import, visualize, and manipulate the S-parameters of an RF network. Read and write multiport Touchstone files. Create and analyze networks of lumped and distributed components such as matching and feed networks. Get started with electromagnetic analysis of planar PCB components.
Published: 19 Jun 2023
Thanks, Joseph. And welcome, again, from my side. And thanks, Joseph, for the kind introduction.
And so this is actually the first time that I have the opportunity to give a talk on RF for scientific applications. So I'm very excited about it. So what I'm sharing here on the screen is a model that we developed together with a European spallation source of a plasma accelerator. It includes a resonant cavity, including the detuning caused by Lorentz force.
It is quite a sophisticated model. We have an entire RF lineup. We have the control system. We have the modeling, physical modeling of the cavity as well. And I will use this model as a source of inspiration and will walk you step by step through the process that was followed to develop such a model. So hopefully, this will serve you as an inspiration as well to use MathWorks tools, Matlab and Simulink, in your daily job.
And so I decided to break the presentation in three parts. So we will start from the basics of RF data analysis. If you work in the RF domain, you will have, for sure, to deal with lots and lots of measurement data, or data sheets, or information that gets passed to you either by supplier, providers, customers, or by your colleagues, or maybe measurements that you perform in the lab. So we'll see how Matlab-- and RF Toolbox, in particular-- can help you with managing this data.
And then, we will enter, in the next two sessions, more into the details of RF system design. We will start by taking a chain, analyzing it, looking at the different specifications and performance of the chain itself, and then we will see how to integrate this RF chain into a bigger system-- into a system that has multiple feedback loops, that has the best control algorithms, such as this model that I was talking about where we have, essentially, the entire signal generation with multiple references, where we have, essentially, the entire lineup in terms of amplifiers, RF components, where we have essentially, as you can see here, systems to measure the phase, the reference phase of your line, and as well as control the phase with control feedback loops, as well as physical systems that allow you to model the entire RF chain in terms of amplification and signal generation, as well as the physical modeling of the cavity by a resonant component-- in this case, an inductor and a capacitor.
So you can see this is a fairly advanced model. You see that we have multiple feedback loops. So we have one external feedback loop, essentially, and we have a one internal feedback loop to model the detuning. So this is the external feedback loop is for the control, and the internal feedback loop is for the detuning, essentially, where the characteristics of your cavity change as a function of the signal that is applied to the cavity itself.
And then we can, of course, look at different characteristics. And, of course, it comes up on the other window. So you can see, for example, as you run the simulation-- let me make it a little bit bigger-- how the voltage at the terminal of the cavity changes as a function of the instantaneous excitation, as well as how your control algorithm applies.
Good, so we will end here. This is where we end up. This is where we will conclude. But before getting there, we will see all the steps. And in particular, we will start with the RF data analysis.
So what do you start? Good place where to start is actually-- let me just go back for a second to Matlab. I'm going to quickly close the model. We are going to open it up later. And yes, let's stop it and close it. We don't need it right now. And let's go back to Matlab for a second.
A good place where to start, it is also-- clear all my variables that I have in the workspaces so we have a nice clean setup. And a good place for us to start is with, simplest of all, is from the Help, which is just a second for Matlab to clear all the variables. OK, good.
So if you type in help ref, you see all the functions that the Ref Toolbox provides you to manipulate your RF system. And there are a lot. So what do you have?
You have the ability to create objects-- like S-Parameters, objects. You have lots of functions to manipulate the S-Parameters, to transform the S-Parameters-- for example, transformation from S, from scattering parameters, to Z, to impedances or to admittances, or different types of transformations, such as hybrid or ABCD, in terms of state space representation.
We have functions to analyze the passivity, to enforce the passivity, to check the causality. We have functions to fit the characteristics in the frequency domain. We will talk more about it. Of course, to measure the gamma in, the gamma out-- so the input-output characteristics of networks-- as well as to measure the SWR. To write S-Parameters-- I would say that this is probably the most used function, to read and to write touchstone files. And, to plot data-- plotting the rough domain, as well as is in the Smith chart.
And you can build networks. We will talk about it-- so how you can create, really, another network for your analysis so you can stitch together multiple components, and you also have other types of components such as passive distributed components-- such as transmission lines, waveguides, and so forth-- that help you in creating a network beyond just lumped components such as resistors, capacitors, and conductors.
So let's say that we want to very simply load-- and let's just go up-- load an S-Parameter. file. How easy it is well? I'm, going to do use the command S-Parameters. And in this case, I know that I have on the path a default to S to P file. So this is a touchstone file, S-Parameters with two ports. This has come with a rough toolbox, so I know it's always on the path.
So as soon as I type in S equal to S-Parameters. I get my object that has two ports, 191 frequencies, and then it's a 2-by-2 S-Parameters So it's two ports. So it's 4 S-Parameters, refer to a reference impedance of 50 ohms.
So it can't get easier than this, to read S-Parameters and to plot S-Parameters. So if you do a rough plot of S, for example, what we get is a figure with the 4 S-Parameters. So you see here the S11, the S22, the S121. And you can also click here on the legend, essentially, to enable or disable which of the S-Parameters you can visualize.
And, of course, RF plot has a lot of functionality. So for example, you can visualize the angle, I believe, for the S-parameters. If you want to look at the phase. By default, it shows the magnitude and so forth. So again, just a few lines of Matlab code to visualize on the Cartesian coordinates. And if you want to visualize it on the Smith plot, then, again, it cannot be easier. I can just visualize, Yes, the S, Scattering Parameters.
This one is the S11, you can see it here on the plot is a polar representation of visualization of the S-Parameters. And then, you can essentially double-click on the trace, and then you can see different characteristics. So for example, we see here the S-Parameters, the S11 at 2.5 gigahertz for this specific file.
So where to get started? Help RF, lots of functions. Of course, you can always highlight the function, click F1, function key 1, and then, essentially, you will get details about the syntax, how to use it. Everything is documented, and you can figure out, essentially, how to use it.
And that's-- and as you read the touchstone files with an arbitrary port, number of ports-- in this case, it was just the two ports because S2P-- but you can read any Touchstone file with any arbitrary number of ports, and you can also write it with RF write. We will see that.
Good, so what can we do now that we have the S-Parameters? Well, one of the most interesting things that you can do is, essentially-- or one of the most frequent things that you want to do once you have data-- is not only to look at the data just with it right now, but it's also to combine data. So let's say that I have these S-Parameters, and I want to see how a network would behave with these S-Parameters when closed on certain impedances or certain resistor capacitors, and any kind of network. Or, for example, you have multiple S-Parameters coming from data sheets, and you want to cascade them to look at the lineup.
The best way to do it is by creating a circuit-- and it's literally an object called Circuit-- adding the components by defining the terminus at which the components are connected, then defining the ports on which you want to perform the analysis, and then just do the analysis. And as long as we talk about passive networks-- or, I should say, more than passive, linear networks, networks that can be described by components, linear components such as S-Parameters, RLC, or PCB components-- S-Parameters provide all the necessary and sufficient information to describe your network.
This is, by the way, an example, the directory comes from our documentation, but I'm going to use a different example to show how to create a circuit. So let's see a little bit in action. In this case, I'm going to read four different touchstone files. So you see, it's going to be a coaxial cable that has one port, an elbow or a band that has two ports, a coupler with four ports, and, again, an adapter with two ports.
I'm going to import the data, the touchstone files using, again, Command S-Parameters. And then, I'm going to create a circuit, like I was saying. I create a circuit object indicated by the variable ckt with the name Circuit, as I don't have a lot of imagination. And then I'm simply going to connect the components that I imported or the data that I imported, essentially, into our circuit, and defining port 1 and port 7 as the ports of the analysis, and then, essentially, compute the S-Parameters, and potentially write it on a touchstone file that I'm going to call line.s2p.
So let's go back to Matlab. Let's see this one in action. So I'm going to, again, clear all the variables, and I'm going to go just to see it in action. So what you see here, I here have my file, my script. It's called test bench. I have my four S-Parameter files. I'm simply going to step through the section by one.
So first of all, I'm going to read the data. So if you wonder how coax, the object coax looks like, it's an S-Parameter object with one port. So you see it's a 1 by 1 matrix defined over 200 frequency points.
By the way, if you open, if you're not familiar with Touchstone files, if you look at it, they are ASCII files that are standard format. And essentially, here in the header, you see the definition of the data. So the first column is always the frequency. S-Parameters are always defined in the frequency domain. And then, you get the real and imaginary part, or the magnitude and phase information for each of the S-Parameters.
So this is where one port, S-Parameters. If I would open up a four-port S-Parameter, the format is equivalent. So again, you have the header that describes what is the data that you're reading about, and then, in this case, because it's a four-port, it's 16 S-Parameters. So it's a 4-by-4 matrix representing the S-Parameters.
We have the data. We create our circuit. So let's call Circuit. It's a circuit element without any element, so it doesn't have anything inside. And then, in the next part, in the next section here, I can just add the different components.
So in this case, I include my component between port 1 and port 2, elbow between port 2 and port 3, 3, 4, 5, 6, because it's a six-port coupler, the couple of resistors to the terminal of the coupler that I'm not using, and the waveguide here at the end between port 4 of the coupler and 7. And this is, essentially, how my circuit now gets composed out of the different elements. So you can see here which nodes we have and which components we have instantiated.
At this point in time, essentially, the only thing that is left to do is to define what is the frequency range over which we are going to analyze this network. In this case, it's between 347 and 357 megahertz, with 51 frequency points. We're going to define through which ports we're going to perform the S-Parameters analysis-- in this case, port 1 and port 7. 0 represents the ground so it's always the reference. And then, we are going to essentially plot, in this case, using RFplot, like we saw before, the behavior of the network we just created.
Analyze, it I get two figures here on my other screen. So this is the phase. This is the magnitude in dB of our network. You see, it's a little bit jittery because it depends on the resolution at which you provided the S-Parameters. And then, let me just delete this file here just to show you that we create a new file where we store the S-Parameters as. And we save it in a Touchstone file, standard-compliant touchstone file, line.s2p.
And so that's really as simple as it can get to just read the network, read data, create a network, analyze it, and visualize the results. You might wonder, what's the advantage of using a syntax like this, so that is all programmatic? Well, the advantage is that if you want to perform this analysis multiple times, you can very easily script it, automate it.
So let's say that you want to do a for loop sweeping different values of the resistor. You can just do a simple for loop in which you instantiate different values of the resistor, and you can perform a sensitivity analysis of the performance of your network. If you want to share this network with your colleagues, essentially, you can show them or give them the script so they can see exactly how the network were composed, step-by-step.
So it's very traceable, it's reproducible, and it can be automated. And then, last but not least, from here, you can very simply create a report using the Publish command. So very simply, you can just go here, publish the script, and you will get a PDF or a PowerPoint or a Word document capturing your entire script, including the results and the visualization.
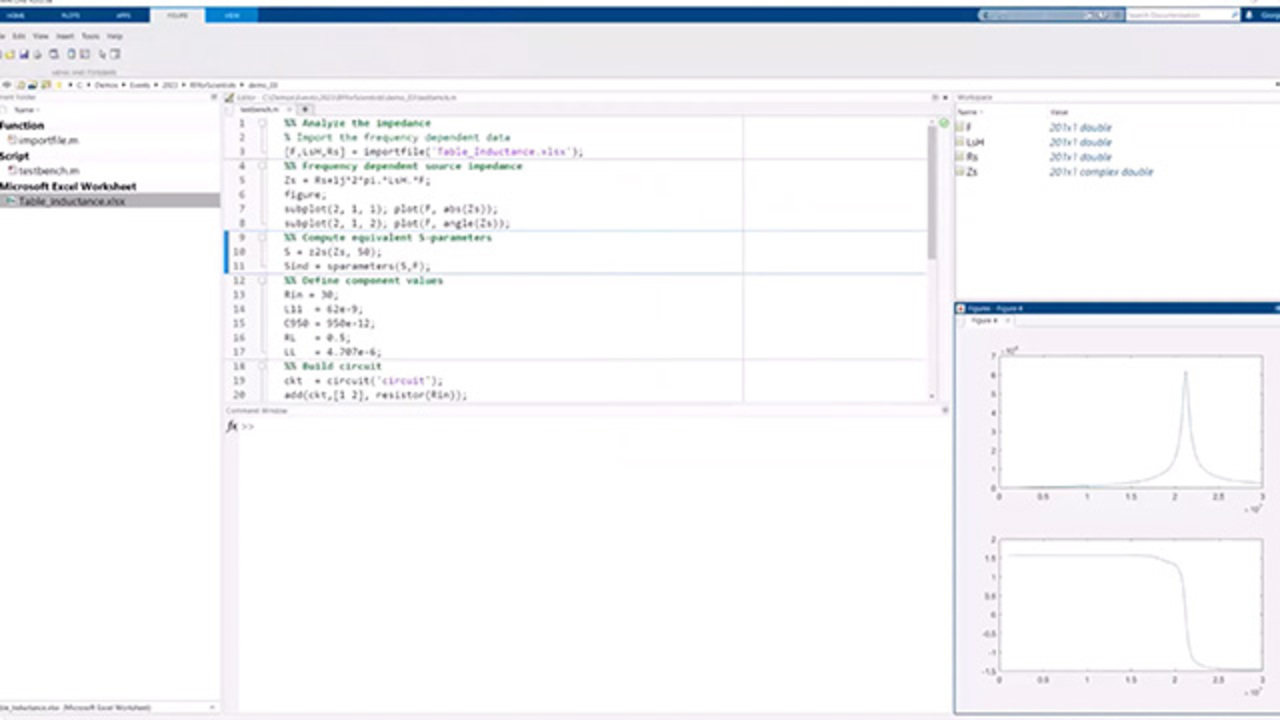
Another example that I find interesting is-- and these are all actually examples that I've worked on from customers and from different situations. In this case, there was a user that had an Excel file where they had the frequency-dependent data for an inductor. So it was a complex, let's say, piece of semiconductor in which he had a frequency-dependent impedance, as well as frequency-dependent admittance, and he stored this into an Excel spreadsheet.
So one of the advantages of working in Matlab is that Matlab is very good in reading different data formats or getting data from anywhere. So we can just import the data. And so in this case, we see we just go from the Excel spreadsheet to three columns of data-- the frequency, the impedance, and the resistance, essentially-- the resistance and admittance.
You can just create an equivalent impedance, ZS, using, essentially, traditional representation. From here, from an impedance, we can use the function S Z to S, so to transform an impedance when S. Use it, for example, to create a circuit, add it to a circuit, add other additional network components, and then, again, analyze it and look at the results.
Let me just quickly go back to Matlab. I'm going to close my example here. I'm trying to keep an eye on the chart, but if you don't see it, please, just wave to me or just say something.
So let's go to our next example, next simple example. I broke down this presentation in lots of small examples so it becomes easier. To share, I'm going to clear my workspace, open up, again, a new test bench. So in this case, you can see here, we have an Excel spreadsheet. Let's look at data outside Matlab.
It's [AUDIO OUT]
--of the measurement. And if you scroll down, you will see that we have lots of data points with different values. From here, we can just import our data file, get the three columns into three variables, F, L, and R, and we can just now create, essentially, a frequency-dependent impedance, and Z S.
We can, of course, visualize it. One of the biggest learned lessons or the biggest advice that I can give you is, whenever you deal with data, with measurement data or with data that either you measure yourself or you are getting from somebody else, my advice is always look at the data, and look at the data in as many ways as possible. So look at data in the magnitude and phase on the real imaginary part, look at it in the frequency domain, look at it in the time domain, look at the spectrum, look at the power characteristics. Because often, you gain a lot of insights by just gaining confidence on what is the meaning of your data.
So in this case, we can, for example, look with a figure-- here, the magnitude and the angle of our admittance, or our impedance, Z S. Transform it to S-Parameters. So in this case, instead of using-- we still use the Command S-Parameters, but instead of using a Touchstone file, we just provided, essentially, the data and the frequency over which the data is provided.
We defined a few more new components-- a resistor, inductors, a capacitor, another resistor, another inductor-- and then we add all these components, including our S-Parameters, to a circuit. We create a network. We analyze it, and then, again, we can expect the results of our network. So this is the input impedance seen from port 1 of the entire network, where we put together the different components. And again, this gives us an information about how the circuit is going to behave. And once we have these S-Parameters, because the network is linear, you can just use it as a representation of your entire network.
And so far so good. This is really getting started, really starting with the basic-- reading data, using data, if you like, visualizing the data, putting it together into a network, storing it, potentially, into a Touchstone file. What's next?
Well, often, what you want to do is, let's say that you have S-Parameters or a transfer function of a network. You want to use it. You want to use these S-Parameters, and you want to use them, for example, to see how the network reacts to a step or to an impulse.
[AUDIO OUT]
--be used in the time domain. Something has to happen to the network to that data. You can't just use the data as it is.
So if you are an engineer, you probably think, oh, I'll just do an inverse FFT. To get my frequency domain data, do an inverse FFT, and I get the time domain waveform. And then, I can use that, essentially, as a filter, and I can use the inverse, the results of the inverse FFT, as the tops of a filter that I can just apply to my waveform.
And this-- I'm going to say this is a brute force approach, but it's an approach that is also very error-prone and can be a source of a lot of problems. And why? A number of things can go wrong, but the major one is that when you do an inverse FFT there is no guarantee that your result is going to be causal. In other words, it can happen that you send an impulse through your filter, and you get an output before the signal at the input actually happens in a system that looks in the future.
Another way of looking at it is that the inverse FFT doesn't really know anything about timing it doesn't really know about what happens at DC because we know, don't have S-Parameters that DC, doesn't have causality for enforcement. So a better way to do that is actually to use a rational fitting. And "rational fitting" essentially means extracting an equivalent pole-zero representation that feeds our frequency domain behavior.
Once we have a pole-zero representation or a state-space representation of a system, we can very easily use it for time domain simulation. So we can use it for streaming signals, for seeing the results of your network when excited, with a step proposal modulated wavefront.
Additionally, because with the poles in the 0 you can force the poles to be on the left-hand side of the complex plane, which means that you can enforce causality. The other advantage is that because this is based on fitting, you essentially can apply a model-order reduction, which means you can keep only the dominant poles-- which means that you don't overfit the waveform, which means that you don't fit noise, for example. That is an undesired behavior.
In other words, you provide-- think about the action of fitting as providing an equivalent representation of your S-Parameters using physical components, like inductor and capacitors, that provides your network to be physically realistic and close to your actual system behavior. The disadvantage, of course, is that when you have distributed components, you will have a lot of poles and lots of zeros that goes with that. But you will have a representation that is stable, that is causal, and on which you can also enforce properties such as passivity.
So let's go back to the line. You remember that we created the line S-Parameter files by cascading our network. In this case, I'm going to re-import it in a new example. I'm going to check passivity and causality. I'm going to compute the transfer function and fit it using a rational representation. And then we're going to use the rational representation for streaming signal.
Let me go back to Matlab. OK, let me do a little bit of cleanup. Again, clear all-- I'm going to clear all the variables, close my figures, close my test bench, and then I'm going to go to our next simple example.
Want to type, just let me know. Raise your hand or give some kind of signal so that we can include you.
Thanks Joseph, indeed. I try to keep an eye on the cat, but I might be missing it. And please, don't be shy. That's the bottom line.
So what we do here, again, we import our Line Touchstone file. We have a couple of functions that are very interesting. We are going to check if it's passive. So in this case, it's a 1, so it means, yes, it's passive.
We can also do-- in the case it was not passive, we can also check where is not passive by using the function passivity. This is an interesting function. Sometimes, you have just a single data point that-- sorry, let me just let me just clean up a little bit.
We just have a single data point-- there we go-- now, where the passivity is infringed. In this case, we can see that the norm of our data is below 1, which means that the data is all passive, just like we said before. So it's all passive.
Because it's passive, we actually already know that it's causal. So it's good data, in a way. But sometimes, it can happen that if you perform measurements and there is something wrong with the calibration procedure or the embedding, the data might turn out to be not causal. And this function will help you to flag it upfront, to know that there is something wrong in your measurement.
We're going to use another function to transform the S-Parameter. So we have seen before Z to S, S to Z. Now, we're looking S to TF. So we're going to compute the transfer function, and we're going to fit the transfer function into an object that we call R.
And by the way, here, I'm fitting the transfer function. I could fit directly to the S-Parameters, and I would get four different fittings-- so one for S11, S12, S21, and S22, of course. And in this case, I'm just interested in the transfer function. So I'm just looking at the rational fitting object, and I see that I can fit these S-Parameters with just four poles.
And once I have the rational object, now I can do very interesting things. I have an equivalent state-based representation pole and zero. I can start sending signals through this object.
So in this case here, everything happens here at line 15. I'm going to compute the time response of our rational fit object r to our input waveform in. In is an array, so you can see that in has 1,000 elements. It has a 500 0s followed by 500 1s, so it's essentially a very simple step response.
And we need to provide, also, what is the timestamp at which the signal is defined? So we know that this vector in is defined with a resolution of 1 divided by 350 megahertz divided by 8. Why 350 megahertz? Well, because if I do a ref plot of S, I can actually see that my data is defined-- I have it here-- around 350 megahertz.
So to actually compute accurately compute the result or the response of the network, I need to have a timestamp that is smaller than the center frequency at which I want to compute the result. Essentially, you need to make sure that you have a timestamp that is small enough. So in this case, we apply an oversampling factor of 8.
OK, so let's look at it. Let's compute the time response. And we're going to plot here the input step. So it's very simple. It's the blue line that you see here that goes from 0 to 1. And here, you can see that you write the response of our network-- I'm going to zoom in here-- you will see the timing, essentially, and the ringing that is the response of the network to our step, essentially. It's the step response of our system, because you can do a pulse response, an impulse response, a step response, or you can send 0s and 1s through your network.
And so far, so good. Just we've covered the very basic things. Now, let's go into a little bit more advanced things that you might be interested in.
We saw how to create a circuit, but what if we want to create a matching network? For example, you have data that comes in, and you want to create an input matching to make sure [AUDIO OUT]
--what does it mean at ? Well, if I go to Matlab, here, right at the top, you see we have many apps. I have pretty much all the MathWorks products installed, so I have a lot of them. But in the section that says the Signal Processing and Communication, in alphabetical order here, you will find the Matching Network Designer App. In this case, I pinned it to one of my favorites.
In this way, with the Matching Network Designer App, essentially, you can decide-- you can provide the input characteristics of your data, and then you can decide to design a matching network given a set of constraints, such as the matching bandwidth of the return-loss level. And then you can choose the architecture, if it is a pi or a T network. And then, you can cascade multiple networks if you want to increase the matching bandwidth.
What else can you do? Often, when you work in the RF domain, you develop PCBs. So you use distributed components on PCBs.
What you can easily do-- and we will see a very simple example-- is to design PCB components. And you can actually fabricate them. And from these components, you can generate Gerber files for fabrication. And you can include them in your test setup or in your experiment, let's say.
So which type of components? Well, you have different type of components, from inductors-- you see here different shapes, interdigital capacitor, or different structures of capacitor couplers, lines, filters, splitters, different types of structures or stubs, funds, and types of structures to improve, then, the matching, for example.
These are all distributed. You can design them to operate at a certain frequency. You can analyze them using a full-wave electromagnetic analysis. We will see that, and then we can combine them into a larger PCB, and we can fabricate them. And again, we can also insert them or include them in a circuit. We see a simple example right now.
So what are we going to do now? We are going to design a couple of branch lines to operate, in this case, at 3 gigahertz. And we are going to-- you can see that we have a function here that is called Design. Design is a function that automatically scales the geometry of an element to make it operational at the given frequency.
So we start with the default configuration that you see here. After the design function, you see how the line width and geometrical properties of the object have changed to make it operating at 3 gigahertz. And then, we can compute the S-Parameter. [AUDIO OUT] --gets analyzed with the method of moment, or full-wave electromagnetic simulation.
So again, let me Clear All. Let me clear my screen, and I'm going to jump to one more example here. So let's do that. In that way, you might wonder, OK, a couple of branch lines. Are there many other components? I showed a few. Let me just give you a little bit more details.
So we have a product that is called the RF PCB Toolbox, where you have all these catalog components. That's interesting. So if you go to the section on RF and mixed signal of the documentation, I think my computer or my internet connection, one of the two is very slow. But just bear with me,
I go to the RF PCB Toolbox. And then, you can see here, we have the PCB component catalogs. And we have different type of components, like a transmission line, filter, splitters, couplers-- all these type of structures. And by the way, every release, you will find new components added to the catalog.
So in this case, a branch line coupler, I took it from this section here, where you can see we have a family of different types of couplers and splitters, different types of properties. And that's what it comes from.
So as soon as I do coupler, branch line, I create an object that is called coupler. That is my coupler branch line. You see here, these are all the properties, and I can actually change each of these properties to scale the geometry manually, if you like.
You can also decide to, for example, do a for loop analysis-- let's say, let's sweep all the arm's length between a certain value and the certain value. Or, you can insert it in an optimization algorithm. So let's look at our coupler, and go ahead and just execute the first couple of lines. There we go.
I'm just getting up a few things here. Of course, it appears on the other desktop. There we go.
And we can now change the coupler height-- for example, just to give an example of changing one of the characteristics. So you see how, essentially, again, with a command-line approach, you can easily iterate. So in this case, we changed the height from 1.6 millimeters to 0.5 millimeters.
Again, we can look at the coupler, or we can design the coupler. This is probably a little bit more interesting. So let's just execute this next two lines of code where we design the coupler to be resonant at 3 gigahertz.
We can look at the coupler. You can see that the geometry has changed. And if I look, now, coupler here, you will see that the properties are-- all the geometrical properties have changed compared to before, then make it operating at 3 gigahertz. And now, we can actually analyze it using the method of moment. So now, what happens behind the scenes is we see here that we calculate the 21 frequency points over which we are going to analyze the coupler between 1 and 5 gigahertz.
So what's happening behind the scenes is that, essentially, the structure gets meshed. It gets automatically divided in smaller units. There are triangular triangles for the surface. They're tetrahedral for the volume. And this mesh is used to compute the field properties using the method of moments.
You can also define different material properties. You can, for example, say the dielectric has different relative permeability or different loss tangents. We provide, again, a catalog of materials, but you can also define your own component, as well as you can define the different conductivity properties for the metallization of your PCB.
And, of course, if you're familiar with electromagnetic analysis, you can also manually mesh the network. You can enforce a different maximum or minimum edge length, as well as a growth ratio from minimum to maximum. By default, the solver uses a maximum edge length that is 1/10 of the maximum operating frequencies. In other words, it uses a 10 wavelengths per-- 1/10 of the wavelength for the maximum edge length. And this guarantees that, essentially, in general, the results are accurate enough for your simulation.
Good, and so in the meantime-- oops, where are we? The simulation is getting to a conclusion. It takes a little bit of time on my computer, but it's not really representative. I'm running on a laptop that is five years old, and I'm suffering a little bit from, I'm going to say, supply chains problem, let's say. What you see here is that, indeed, the copper is well matched at 3 gigahertz.
So this is the port characteristics. A deep notch means that it's matched. And we also see that we have a relatively small insertion loss on the forward characteristics of the itself.
So even if you are not an expert in electromagnetic analysis or in PCB design, you can see how rapidly you can get started. And similarly, you can design, for example, in this case, a spiral inductor with a certain number of turns, with a certain shape-- in this case, it's an octagonal shape for a spiral inductor.
And again, we can compute the S-Parameters of this inductor. But what I really want to point you to is that not only you can compute the S-Parameters using the method of moments. You can also use the compute the S-Parameters using a behavioral representation of the S-Parameters. Essentially, the structure gets represented by small segment.
It's like, think of a behavioral model that is used behind the scenes, with the advantage of a much, much faster simulation. So instead of meshing the entire structure and computing an entire structure, you can have a first pass to your design using a behavioral model. And the results are an approximation, of course. They are not the same. If it would be the same, there would be no need for electromagnetic analysis.
But in first pass, in terms of order of magnitude, the results are good enough for a first pass of the design. And then, of course, once you have a PCB element-- in this case, it could be an inductor. It could be the coupler. It could be anything that you have designed from the PCB Toolbox-- again, you can bring it back into your circuit. You can connect it with other components-- a lamp, or distributed, or S-Parameters. And then, essentially, you can again verify the behavior of your network, essentially.
So what we have seen, essentially, we talked about the adding PCB components. We briefly talked about the behavioral analysis that the catalog components provide and the ability, essentially, to put it as part of a circuit. I'm getting now towards the end of the first part of the presentation, on how to get started. Just want to give you a reference.
We have a very good series. There's five videos that you find online, Getting Started with S-Parameters. I really recommend you to check it out in case you have never used Matlab for S-Parameter analysis or for data analysis. It's a good starting point, and, of course, we have lots and lots of examples.