RF Design of Wideband mmWave Beamforming Systems
Overview
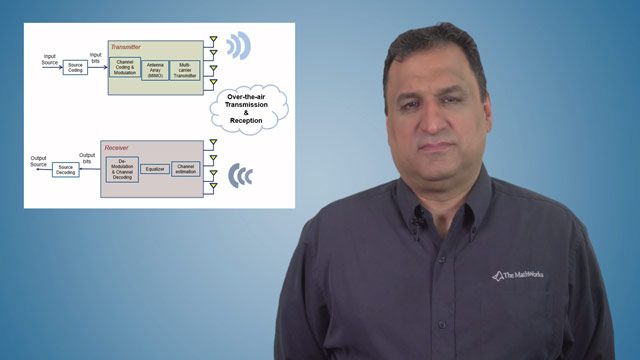
The current trend for wireless systems to operate at millimeter wave (mmWave) frequencies and over wide bandwidth drives challenging requirements for RF front ends. In this webinar, you will learn how MATLAB and Simulink can be used for modeling RF and mmWave transceivers, performing RF budget analysis, and simulating wideband adaptive architectures. These will include RF components such as amplifiers, matching networks, and antenna arrays operating at mmWave frequencies.
Using virtual prototypes, we will simulate wideband transmitter and receiver behavior including co-existence and interference scenarios along with beam-squinting and antenna coupling. These same virtual prototypes will be used to perform dynamic EVM measurements for different communications standards such as 5G FR2.
With practical examples, we will demonstrate how to optimize baseband signal processing algorithms and control logic together with RF transceivers to compensate for RF impairments, to compensate for RF impairments, improve overall receiver sensitivity in the presence of interfering signals, and to support multiple communication standards.
Highlights
Topics that will be covered include the following:
- Introducing MIMO RF front-end design including antenna arrays
- Integrating antennas and PCB components into RF front ends
- Modeling wideband mmWave beamforming RF transmitters and receivers
- Simulating co-existence and interference scenarios
About the Presenter
Giorgia Zucchelli is the product manager for RF and mixed-signal at MathWorks. Before moving to this role in 2013, she was an application engineer focusing on signal processing and communications systems and specializing in analog simulation. Before joining MathWorks in 2009, Giorgia worked at NXP Semiconductors on mixed-signal verification methodologies and at Philips Research developing system-level models for innovative communications systems. Giorgia has a master’s degree in electrical engineering and a doctorate in electronics for telecommunications from the University of Bologna.
Recorded: 16 May 2023