lqr

Diseño de un regulador lineal cuadrático (LQR)

Sintaxis

[K,S,P] = lqr(sys,Q,R,N)

[K,S,P] = lqr(A,B,Q,R,N)

Descripción

[K,S,P] = lqr(sys,Q,R,N) calcula la matriz de ganancia óptima K, la solución S de la ecuación algebraica de Riccati asociada y los polos de lazo cerrado P para el modelo de espacio de estados en tiempo continuo o tiempo discreto sys. Q y R son las matrices de ponderación para estados y entradas, respectivamente. La matriz de término cruzado N se establece en cero cuando se omite.

[K,S,P] = lqr(A,B,Q,R,N) calcula la matriz de ganancia óptima K, la solución S de la ecuación algebraica de Riccati asociada y los polos de lazo cerrado P utilizando las matrices de espacio de estados en tiempo continuo A y B. Esta sintaxis solo es válida para modelos de tiempo continuo. Para modelos de tiempo discreto, utilice dlqr.

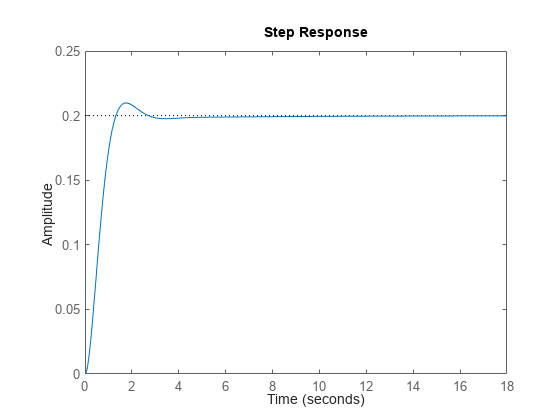
Ejemplos

Control LQR para modelo de péndulo invertido

pendulumModelCart.mat contiene el modelo de espacio de estados para un péndulo invertido en un carro donde las salidas son el desplazamiento del carro x y el ángulo del péndulo $\theta$. La entrada de control u es la fuerza horizontal sobre el carro.

$$\begin{array}{l}\left[\begin{array}{c}\underset{}{\overset{\dot{}}{x}}\\ \underset{}{\overset{¨}{x}}\\ \underset{}{\overset{\dot{}}{\theta }}\\ \underset{}{\overset{¨}{\theta }}\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -0.1& 3& 0\\ 0& 0& 0& 1\\ 0& -0.5& 30& 0\end{array}\right]\left[\begin{array}{c}x\\ \underset{}{\overset{\dot{}}{x}}\\ \theta \\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]+\left[\begin{array}{c}0\\ 2\\ 0\\ 5\end{array}\right]u\\ y=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}x\\ \underset{}{\overset{\dot{}}{x}}\\ \theta \\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]u\end{array}$$

Primero, cargue el modelo de espacio de estados sys en el área de trabajo.

load('pendulumCartModel.mat','sys')

Puesto que las salidas son x y $\theta$, y solo hay una entrada, utilice la regla de Bryson para determinar Q y R.

Q = [1,0,0,0;...
    0,0,0,0;...
    0,0,1,0;...
    0,0,0,0];
R = 1;

Encuentre la matriz de ganancia K utilizando lqr. Puesto que N no se especifica, lqr establece N en 0.

[K,S,P] = lqr(sys,Q,R)

K = 1×4

   -1.0000   -1.7559   16.9145    3.2274

S = 4×4

    1.5346    1.2127   -3.2274   -0.6851
    1.2127    1.5321   -4.5626   -0.9640
   -3.2274   -4.5626   26.5487    5.2079
   -0.6851   -0.9640    5.2079    1.0311

P = 4×1 complex

  -0.8684 + 0.8523i
  -0.8684 - 0.8523i
  -5.4941 + 0.4564i
  -5.4941 - 0.4564i

Aunque la regla de Bryson suele ofrecer resultados satisfactorios, normalmente solo es el punto de partida para un procedimiento de diseño iterativo de prueba y error para ajustar la respuesta del sistema de lazo cerrado en función de los requisitos de diseño.

Control LQR utilizando matrices de espacio de estados

aircraftPitchModel.mat contiene las matrices de espacio de estados de una aeronave donde la entrada es el ángulo de deflexión del elevador $\delta$ y la salida es el ángulo de inclinación de la aeronave $\theta$.

$$\begin{array}{l}\left[\begin{array}{c}\underset{}{\overset{\dot{}}{\alpha }}\\ \underset{}{\overset{\dot{}}{q}}\\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]=\left[\begin{array}{ccc}-0.313& 56.7& 0\\ -0.0139& -0.426& 0\\ 0& 56.7& 0\end{array}\right]\left[\begin{array}{c}\alpha \\ q\\ \theta \end{array}\right]+\left[\begin{array}{c}0.232\\ 0.0203\\ 0\end{array}\right]\left[\delta \right]\\ y=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\left[\begin{array}{c}\alpha \\ q\\ \theta \end{array}\right]+\left[0\right]\left[\delta \right]\end{array}$$

Para una referencia de escalón de 0,2 radianes, considere los siguientes criterios de diseño:

• Tiempo de subida inferior a 2 segundos

• Tiempo de establecimiento inferior a 10 segundos

• Error de estado estacionario inferior al 2%

Cargue los datos del modelo en el área de trabajo.

load('aircraftPitchModel.mat')

Defina la matriz ponderada de coste de estado Q y la matriz ponderada de control R. Por lo general, puede utilizar la regla de Bryson para definir las matrices ponderadas iniciales Q y R. En este ejemplo, considere el vector de salida C junto con un factor de escalado de 2 para la matriz Q y elija R como 1. R es un escalar porque el sistema solo tiene una entrada.

R = 1

R = 
1

Q1 = 2*C'*C

Q1 = 3×3

     0     0     0
     0     0     0
     0     0     2

Calcule la matriz de ganancia utilizando lqr.

[K1,S1,P1] = lqr(A,B,Q1,R);

Compruebe la respuesta al escalón de lazo cerrado con la matriz de ganancia generada K1.

sys1 = ss(A-B*K1,B,C,D);
step(sys1)

Puesto que esta respuesta no cumple los objetivos de diseño, aumente el factor de escalado a 25, calcule la matriz de ganancia K2 y compruebe la respuesta al escalón de lazo cerrado para la matriz de ganancia K2.

Q2 = 25*C'*C

Q2 = 3×3

     0     0     0
     0     0     0
     0     0    25

[K2,S2,P2] = lqr(A,B,Q2,R);
sys2 = ss(A-B*K2,B,C,D);
step(sys2)

En la gráfica de respuesta al escalón de lazo cerrado, el tiempo de subida, el tiempo de establecimiento y el error de estado estacionario cumplen los objetivos de diseño.

Argumentos de entrada

sys — Modelo de sistema dinámico

Objeto de modelo ss

Modelo de sistema dinámico, especificado como objeto de modelo ss.

A — Matriz de estado

Matriz de n por n

Matriz de estado, especificada como una matriz de n por n, donde n es el número de estados.

B — Matriz de entrada a estado

Matriz de n por m

Matriz de entrada a estado, especificada como matriz de entrada a estado de n por m, donde m es el número de entradas.

Q — Matriz ponderada de coste de estado

matriz

Matriz ponderada de coste de estado, especificada como una matriz de n por n, donde n es el número de estados. Puede utilizar la regla de Bryson para establecer los valores iniciales de Q dados por:

$$\begin{array}{l}{Q}_{i,i}=\frac{1}{\text{maximum acceptable value of }{\left(erro{r}_{states}\right)}^2},\text{ i}\in \left\{1,2,\mathrm{...},n\right\}\\ Q=\left[\begin{array}{cccc}{Q}_{1,1}& 0& \cdots & 0\\ 0& Q_{2,2}& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & Q_{n,n}\end{array}\right]\end{array}$$

En este caso, n es el número de estados.

R — Matriz ponderada de coste de entrada

escalar | matriz

Matriz ponderada de coste de entrada, especificada como escalar o matriz del mismo tamaño que D'D. En este caso, D es la matriz de espacio de estados de alimentación. Puede utilizar la regla de Bryson para establecer los valores iniciales de R dados por:

$$\begin{array}{l}{R}_{j,j}=\frac{1}{\text{maximum acceptable value of }{\left(erro{r}_{inputs}\right)}^2},\text{ j}\in \left\{1,2,\mathrm{...},m\right\}\\ R=\left[\begin{array}{cccc}{R}_{1,1}& 0& \cdots & 0\\ 0& R_{2,2}& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & R_{m,m}\end{array}\right]\end{array}$$

En este caso, m es el número de entradas.

N — Matriz de término cruzado opcional

0 (predeterminado) | matriz

Matriz de término cruzado opcional, especificada como matriz. Si N no se especifica, lqr establece N en 0 de forma predeterminada.

Argumentos de salida

K — Ganancia óptima

vector fila

Ganancia óptima del sistema de lazo cerrado, devuelta como un vector fila de tamaño n, donde n es el número de estados.

S — Solución de la ecuación algebraica de Riccati asociada

matriz

Solución de la ecuación algebraica de Riccati asociada, devuelta como una matriz de n por n, donde n es el número de estados. Dicho de otra forma, S es la misma dimensión que la matriz de espacio de estados A. Para más información, consulte icare e idare.

P — Polos del sistema de lazo cerrado

vector columna

Polos del sistema de lazo cerrado, devueltos como un vector columna de tamaño n, donde n es el número de estados.

Limitaciones

Los datos de entrada deben cumplir las siguientes condiciones:

• El par (A,B) debe ser estabilizable.

• R debe ser definido positivo.

• $$\left[\begin{array}{cc}Q& N\\ N^T& R\end{array}\right]$$ debe ser semidefinido positivo (de manera equivalente, $$Q-N{R}^{-1}{N}^T\ge 0$$).

• $$(Q-N{R}^{-1}{N}^T,A-B{R}^{-1}{N}^T)$$ no debe tener ningún modo no observable en el eje imaginario (o círculo unitario en tiempo discreto).

Sugerencias

• lqr soporta los modelos de descriptores con E no singular. La salida S de lqr es la solución de la ecuación algebraica de Riccati para el modelo de espacio de estados explícito equivalente:

  $$\frac{dx}{dt}=E^{-1}Ax+E^{-1}Bu$$

Algoritmos

En sistemas de tiempo continuo, lqr calcula el control de retroalimentación de estados $$u=-Kx$$ que disminuye la función cuadrática de coste

$$J(u)={\displaystyle {\int }_0^{\infty }(x^{T}Qx+u^{T}Ru+2x^{T}Nu)dt}$$

en función de la dinámica del sistema $$\dot{x}=Ax+Bu$$.

Además de la ganancia de retroalimentación de estados K, lqr devuelve la solución S de la ecuación algebraica de Riccati asociada

$$A^{T}S+SA-(SB+N)R^{-1}(B^{T}S+N^T)+Q=0$$

y los polos de lazo cerrado $$P=eig\left(A-BK\right)$$. La matriz de ganancia K deriva de S utilizando

$$K=R^{-1}(B^{T}S+N^T).$$

En sistemas de tiempo discreto, lqr calcula el control de retroalimentación de estados $$u_n=-K{x}_n$$ que disminuye

$$J={\displaystyle \sum _{n=0}^{\infty }\{x^{T}Qx+u^{T}Ru+2x^{T}Nu\}}$$

en función de la dinámica del sistema $$x_{n+1}=A{x}_n+B{u}_n$$.

En todos los casos, al omitir la matriz de término cruzado N, lqr establece N en 0.

Historial de versiones

Introducido antes de R2006a

Consulte también

icare | idare | dlqr | lqg | lqi | lqrd | lqry | lqgreg | lqgtrack

Temas

• Regulate Pressure in Drum Boiler