Probability density function for Gaussian mixture distribution
Syntax
Description
Examples
Compute pdf Values
Create a gmdistribution object and compute its pdf values.
Define the distribution parameters (means and covariances) of a two-component bivariate Gaussian mixture distribution.
mu = [1 2;-3 -5];
sigma = [1 1]; % shared diagonal covariance matrixCreate a gmdistribution object by using the gmdistribution function. By default, the function creates an equal proportion mixture.
gm = gmdistribution(mu,sigma)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: 1 2 Component 2: Mixing proportion: 0.500000 Mean: -3 -5
Compute the pdf values of gm.
X = [0 0;1 2;3 3;5 3]; pdf(gm,X)
ans = 4×1
0.0065
0.0796
0.0065
0.0000
Plot pdf
Create a gmdistribution object and plot its pdf.
Define the distribution parameters (means, covariances, and mixing proportions) of two bivariate Gaussian mixture components.
p = [0.4 0.6]; % Mixing proportions mu = [1 2;-3 -5]; % Means sigma = cat(3,[2 .5],[1 1]) % Covariances 1-by-2-by-2 array
sigma =
sigma(:,:,1) =
2.0000 0.5000
sigma(:,:,2) =
1 1
The cat function concatenates the covariances along the third array dimension. The defined covariance matrices are diagonal matrices. sigma(1,:,i) contains the diagonal elements of the covariance matrix of component i.
Create a gmdistribution object by using the gmdistribution function.
gm = gmdistribution(mu,sigma)
gm = Gaussian mixture distribution with 2 components in 2 dimensions Component 1: Mixing proportion: 0.500000 Mean: 1 2 Component 2: Mixing proportion: 0.500000 Mean: -3 -5
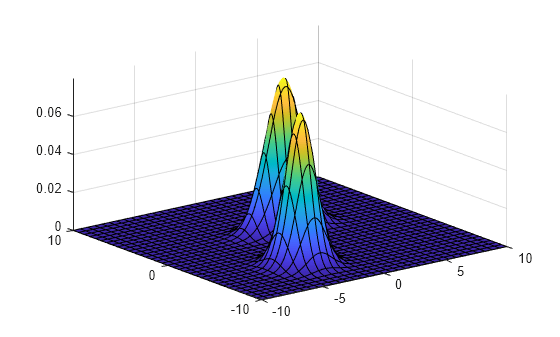
Plot the pdf of the Gaussian mixture distribution by using fsurf.
gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0 y0]),x,y); fsurf(gmPDF,[-10 10])
Input Arguments
gm — Gaussian mixture distribution
gmdistribution object
Gaussian mixture distribution, also called Gaussian mixture model (GMM), specified as a gmdistribution object.
You can create a gmdistribution object using gmdistribution or fitgmdist. Use the gmdistribution function to create a
gmdistribution object by specifying the distribution parameters.
Use the fitgmdist function to fit a gmdistribution
model to data given a fixed number of components.
X — Values at which to evaluate pdf
n-by-m numeric matrix
Values at which to evaluate the pdf, specified as an n-by-m numeric matrix, where n is the number of observations and m is the number of variables in each observation.
Data Types: single | double
Output Arguments
y — pdf values
n-by-1 numeric vector
pdf values of the Gaussian mixture distribution gm,
evaluated at X, returned as an
n-by-1 numeric vector, where n is the
number of observations in X.
The pdf function computes the pdf values by using the
likelihood of each component given each observation and the component probabilities.
where L(Cj|Oj) is the likelihood of component j given
observation i, and P(Cj) is the probability of component j. The
pdf function computes the likelihood term by using
the multivariate normal pdf of the jth Gaussian mixture
component evaluated at observation i. The component
probabilities are the mixing proportions of mixture components, the
ComponentProportion property of
gm.
Version History
Introduced in R2007b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)