Distribución normal multivariante

Visión general

La distribución normal multivariante es una generalización de la distribución normal univariante a dos o más variables. Es una distribución para vectores aleatorios de variables correlacionadas, en la que cada elemento de vector tiene una distribución normal univariante. En el caso más sencillo, no hay correlación entre las variables y los elementos de los vectores son variables aleatorias normales univariantes e independientes.

Como es muy sencillo trabajar con las distribuciones normales multivariantes, se suelen usar como modelo de datos multivariantes.

Statistics and Machine Learning Toolbox™ ofrece varias funcionalidades relacionadas con la distribución normal multivariante.

• Genere números aleatorios a partir de la distribución usando mvnrnd.

• Evalúe la función de densidad de probabilidad (pdf) en valores específicos usando mvnpdf.

• Evalúe la función de distribución acumulativa (cdf) en valores específicos usando mvncdf.

Parámetros

La distribución normal multivariante usa los parámetros de esta tabla.

Parámetro	Descripción	Análogo normal univariante
μ	Vector de media	Media μ (escalar)
Σ	Matriz de covarianzas: los elementos diagonales contienen las varianzas de cada variable, mientras que los elementos fuera de la diagonal contienen las covarianzas entre las variables	Varianza σ2 (escalar)

Tenga en cuenta que, en el caso de una sola dimensión, Σ es la varianza, no la desviación estándar. Para obtener más información sobre los parámetros de la distribución normal univariante, consulte Parámetros.

Función de densidad de probabilidad

La función de densidad de probabilidad (pdf) de la distribución normal multivariante dimensional d es

$$y\text{ = }f(x,\mu ,\Sigma )\text{ = }\frac{\text{1}}{\sqrt{\left|\Sigma \right|{\text{(2}\pi \text{)}}^d}}\exp \left(-\frac{\text{1}}{\text{2}}\text{(}x\text{-}\mu \text{) }{\Sigma }^{\text{-1}}\text{(}x\text{-}\mu \text{)'}\right)$$

donde x y μ son vectores de 1 por d y Σ es una matriz definida positiva y simétrica de d por d.

Tenga en cuenta que Statistics and Machine Learning Toolbox:

• Admite Σ singular solo para la generación de vectores aleatorios. La pdf no se puede escribir en la misma forma cuando Σ es singular.

• Usa x y μ orientados como vectores fila en lugar de vectores columna.

Para ver un ejemplo, consulte Pdf de distribución normal bivariante.

Función de distribución acumulativa

La función de distribución acumulativa (cdf) multivariante evaluada en x se define como la probabilidad de que un vector aleatorio v, distribuido como una normal multivariante, se encuentra dentro del rectángulo semiinfinito con límites superiores definido por x,

$$\mathrm{Pr}\{v(1)\le x(1),v(2)\le x(2),\mathrm{...},v(d)\le x(d)\}.$$

Aunque la cdf normal multivariante no tiene una forma cerrada, mvncdf puede calcular los valores de cdf de manera numérica.

Para ver un ejemplo, consulte Cdf de distribución normal bivariante.

Ejemplos

Pdf de distribución normal bivariante

Calcule y represente la pdf de una distribución normal bivariante con los parámetros mu = [0 0] y Sigma = [0.25 0.3; 0.3 1].

Defina los parámetros mu y Sigma.

mu = [0 0];
Sigma = [0.25 0.3; 0.3 1];

Cree una cuadrícula de puntos espaciados equidistantemente en un espacio bidimensional.

x1 = -3:0.2:3;
x2 = -3:0.2:3;
[X1,X2] = meshgrid(x1,x2);
X = [X1(:) X2(:)];

Evalúe la pdf de la distribución normal en los puntos de la cuadrícula.

y = mvnpdf(X,mu,Sigma);
y = reshape(y,length(x2),length(x1));

Represente los valores de la pdf.

surf(x1,x2,y)
caxis([min(y(:))-0.5*range(y(:)),max(y(:))])
axis([-3 3 -3 3 0 0.4])
xlabel('x1')
ylabel('x2')
zlabel('Probability Density')

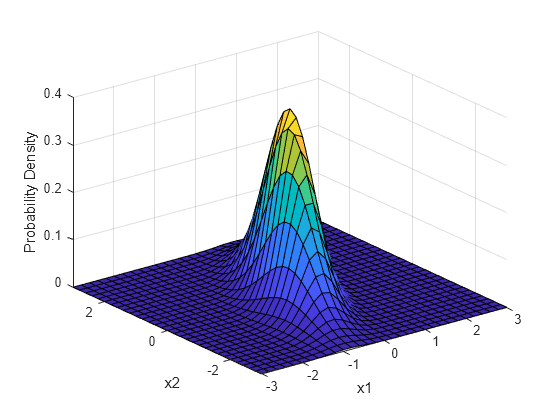
Cdf de distribución normal bivariante

Calcule y represente la cdf de una distribución normal bivariante.

Defina el vector de media mu y la matriz de covarianzas Sigma.

mu = [1 -1];
Sigma = [.9 .4; .4 .3];

Cree una cuadrícula de 625 puntos espaciados equidistantemente en un espacio bidimensional.

[X1,X2] = meshgrid(linspace(-1,3,25)',linspace(-3,1,25)');
X = [X1(:) X2(:)];

Evalúe la cdf de la distribución normal en los puntos de la cuadrícula.

p = mvncdf(X,mu,Sigma);

Represente los valores de la cdf.

Z = reshape(p,25,25);
surf(X1,X2,Z)

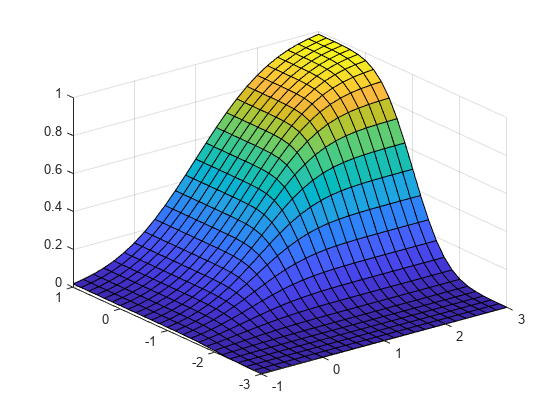
Probabilidad sobre una región rectangular

Calcule la probabilidad sobre el cuadrado de una unidad de una distribución normal bivariante y cree una gráfica de contorno de los resultados.

Defina los parámetros de la distribución normal bivariante mu y Sigma.

mu = [0 0];
Sigma = [0.25 0.3; 0.3 1];

Calcule la probabilidad sobre el cuadrado de la unidad.

p = mvncdf([0 0],[1 1],mu,Sigma)

p = 0.2097

Para ver el resultado, cree una cuadrícula de puntos espaciados equidistantemente en un espacio bidimensional.

x1 = -3:.2:3;
x2 = -3:.2:3;
[X1,X2] = meshgrid(x1,x2);
X = [X1(:) X2(:)];

Después, evalúe la pdf de la distribución normal en los puntos de la cuadrícula.

y = mvnpdf(X,mu,Sigma);
y = reshape(y,length(x2),length(x1));

Por último, cree una gráfica de contorno de la distribución normal multivariante que incluya el cuadrado de la unidad.

contour(x1,x2,y,[0.0001 0.001 0.01 0.05 0.15 0.25 0.35])
xlabel('x')
ylabel('y')
line([0 0 1 1 0],[1 0 0 1 1],'Linestyle','--','Color','k')

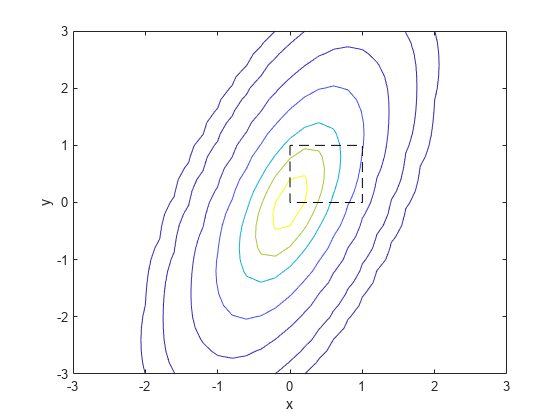
Calcular la probabilidad acumulativa multivariante conlleva bastante más trabajo que calcular una probabilidad univariante. De forma predeterminada, la función mvncdf calcula los valores con una precisión poco inferior a la de una máquina y devuelve una estimación del error como una segunda salida opcional. Consulte la estimación del error en este caso.

[p,err] = mvncdf([0 0],[1 1],mu,Sigma)

p = 0.2097

err = 1.0000e-08

Referencias

[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.

Consulte también

mvncdf | mvnpdf | mvnrnd | NormalDistribution

Temas relacionados

• Distribución normal
• Supported Distributions

×

Abrir ejemplo

Tiene una versión modificada de este ejemplo. ¿Desea abrir este ejemplo con sus modificaciones?

No, sobrescribir la versión modificada Sí