La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

bodemag

Diagrama de Bode de solo magnitud de la respuesta en frecuencia

Sintaxis

bodemag(sys)

bodemag(sys1,sys2,...,sysN)

bodemag(sys1,LineSpec1,...,sysN,LineSpecN)

bodemag(___,w)

Descripción

bodemag permite generar gráficas de solo magnitud para visualizar la respuesta en frecuencia de magnitudes de un sistema dinámico.

Para una función más completa, consulte bode. bode proporciona información de magnitud y de fase. Si tiene System Identification™ Toolbox, bode también devuelve los valores calculados, incluidas estimaciones estadísticas.

Para más opciones de representación personalizables, consulte bodeplot.

bodemag(sys) crea un diagrama de magnitud de Bode de la respuesta en frecuencia del modelo de sistema dinámico sys. El diagrama muestra la magnitud (en dB) de la respuesta del sistema como una función de frecuencia. bodemag determina automáticamente las frecuencias que se van a representar en función de la dinámica del sistema.

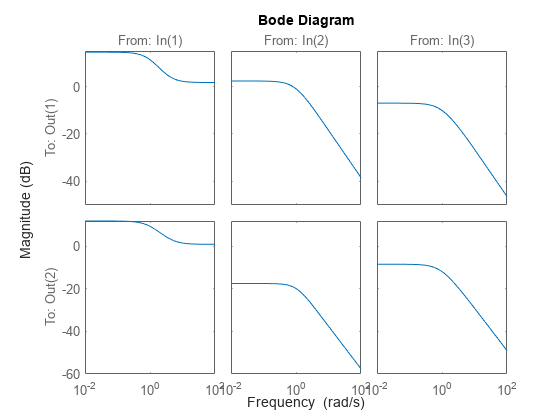
Si sys es un modelo con varias entradas y varias salidas (MIMO), bodemag crea un arreglo de diagramas de magnitud de Bode en el que cada gráfica muestra la respuesta en frecuencia de un par de E/S.

Si sys es un modelo con coeficientes complejos, entonces:

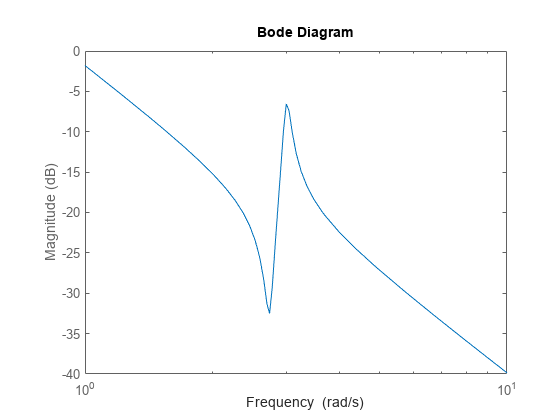
• En la escala de frecuencia logarítmica, el diagrama muestra dos ramas, una para frecuencias positivas y otra para frecuencias negativas. El diagrama también muestra flechas que indican la dirección de los valores de frecuencia que aumentan para cada rama. Consulte Diagrama de Bode de un modelo con coeficientes complejos.

• La escala de frecuencia lineal, el diagrama muestra una única rama con un rango de frecuencia simétrico centrado en un valor de frecuencia de cero.

bodemag(sys1,sys2,...,sysN) representa la respuesta en frecuencia de varios sistemas dinámicos en el mismo diagrama. Todos los sistemas deben contar con el mismo número de entradas y salidas.

bodemag(sys1,LineSpec1,...,sysN,LineSpecN) especifica un color, un estilo de línea y un marcador para cada sistema del diagrama.

bodemag(___,w) representa respuestas de sistema para frecuencias especificadas por w. Puede especificar un rango de frecuencia o un vector de frecuencias. Puede utilizar esta sintaxis con cualquiera de las combinaciones de entrada-argumento de sintaxis anteriores.

Ejemplos

Diagrama de magnitud de Bode de un sistema dinámico

Cree un diagrama de magnitud de Bode del siguiente sistema dinámico SISO de tiempo continuo.

$$\mathit{H}\left(\mathit{s}\right)=\frac{{\mathit{s}}_{}^2+0.1\mathit{s}+7.5}{{\mathit{s}}_{}^4+0.12{\mathit{s}}_{}^3+9{\mathit{s}}_{}^2}$$

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
bodemag(H)

bodemag selecciona automáticamente el rango del diagrama en función de la dinámica del sistema.

Diagrama de magnitud de Bode en frecuencias especificadas

Cree un diagrama de magnitud de Bode a lo largo de un rango de frecuencia especificado. Utilice este enfoque cuando desee centrarse en la dinámica de un rango de frecuencia en particular.

H = tf([-0.1,-2.4,-181,-1950],[1,3.3,990,2600]);
bodemag(H,{1,100})
grid on

El arreglo de celdas {1,100} especifica el valor de frecuencia mínimo y máximo del diagrama de magnitud de Bode. Cuando establece límites de frecuencia de esta manera, la función selecciona los puntos intermedios para los datos de respuesta en frecuencia.

Como alternativa, especifique un vector de puntos de frecuencia para utilizar cuando evalúe y represente la respuesta en frecuencia.

w = [1 5 10 15 20 23 31 40 44 50 85 100];
bodemag(H,w,'.-')
grid on

bodemag representa la respuesta en frecuencia solo en las frecuencias especificadas.

Comparar diagramas de magnitud de Bode de varios sistemas dinámicos

Compare la magnitud de la respuesta en frecuencia de un sistema de tiempo continuo con un sistema discretizado equivalente en el mismo diagrama de Bode.

Cree sistemas dinámicos de tiempo continuo y tiempo discreto.

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
Hd = c2d(H,0.5,'zoh');

Cree un diagrama de magnitud de Bode que muestre las respuestas de ambos sistemas.

bodemag(H,Hd)

El diagrama de magnitud de Bode de un sistema de tiempo discreto incluye una línea vertical que marca la frecuencia Nyquist del sistema.

Diagrama de magnitud de Bode con atributos de línea y de marcador especificados

Especifique el color, el estilo de línea o el marcador para cada sistema de un diagrama de magnitud de Bode utilizando los argumentos de entrada LineSpec.

H = tf([1 0.1 7.5],[1 0.12 9 0 0]);
Hd = c2d(H,0.5,'zoh');
bodemag(H,'r',Hd,'b--')

El primer argumento LineSpec, 'r', especifica una línea continua roja para la respuesta de H. El segundo argumento LineSpec, 'b--', especifica una línea discontinua azul para la respuesta de Hd.

Magnitud de un sistema MIMO

Para este ejemplo, cree un sistema de dos salidas y tres entradas.

rng(0,'twister'); % For reproducibility
H = rss(4,2,3);

En este sistema, bodemag representa las respuestas en frecuencia de solo magnitud de cada canal de E/S en un diagrama diferente y en una única figura.

bodemag(H)

Argumentos de entrada

sys — Sistema dinámico

modelo de sistema dinámico | arreglo de modelos

Sistema dinámico, especificado como un modelo de sistema dinámico SISO o MIMO, o bien un arreglo de modelos de sistemas dinámicos. Puede utilizar los siguientes tipos de sistemas dinámicos:

• Modelos LTI numéricos de tiempo continuo o de tiempo discreto, como modelos tf, zpk o ss.

• Modelos dispersos de espacio de estados, como modelos sparss o mechss.

• Modelos LTI generalizados o con incertidumbre, como modelos genss o uss (Robust Control Toolbox). El uso de modelos con incertidumbre requiere Robust Control Toolbox™.

  • Para los bloques de diseño de control ajustables, la función evalúa el modelo con su valor actual para representar la respuesta.

  • En el caso de los bloques de diseño de control con incertidumbre, la función representa el valor nominal y muestras aleatorias del modelo.

• Modelos LTI identificados, como modelos idtf (System Identification Toolbox), idss (System Identification Toolbox) o idproc (System Identification Toolbox). El uso de modelos identificados requiere System Identification Toolbox™.

Si sys es un arreglo de modelos, la gráfica muestra las respuestas de todos los modelos del arreglo en los mismos ejes.

LineSpec — Estilo de línea, marcador y color

cadena | vector de caracteres

Estilo de línea, marcador y color, especificados como cadena o vector de caracteres con símbolos. Los símbolos pueden aparecer en cualquier orden. No es necesario que especifique las tres características. Por ejemplo, si especifica el marcador y omite el estilo de línea, la gráfica mostrará únicamente el marcador y ninguna línea.

Ejemplo: '--or' es una línea discontinua roja con marcadores circulares.

Estilo de línea	Descripción
"-"	Línea continua
"--"	Línea discontinua
":"	Línea de puntos
"-."	Línea de puntos y rayas

Marcador	Descripción
"o"	Círculo
"+"	Signo más
"*"	Asterisco
"."	Punto
"x"	Cruz
"_"	Línea horizontal
"|"	Línea vertical
"s"	Cuadrado
"d"	Rombo
"^"	Triángulo hacia arriba
"v"	Triángulo hacia abajo
">"	Triángulo hacia la derecha
"<"	Triángulo hacia la izquierda
"p"	Pentagrama
"h"	Hexagrama

Color	Descripción
"r"	rojo
"g"	verde
"b"	azul
"c"	cian
"m"	magenta
"y"	amarillo
"k"	negro
"w"	blanco

w — Frecuencias

{wmin,wmax} | vector | []

Frecuencias en las que se calcula la respuesta, especificadas como uno de los siguientes valores:

• Arreglo de celdas en formato {wmin,wmax}: calcula la respuesta en frecuencias entre wmin y wmax. Si wmax es superior a la frecuencia Nyquist de sys, la respuesta se calcula solo hasta la frecuencia Nyquist.

• Vector de frecuencias: calcula la respuesta en cada frecuencia especificada. Por ejemplo, utilice logspace para generar un vector fila con valores de frecuencia espaciados logarítmicamente. El vector w puede contener frecuencias positivas y negativas.

• []: selecciona automáticamente las frecuencias en función de la dinámica del sistema.

En el caso de modelos con coeficientes complejos, si especifica un rango de frecuencia de [w_min,w_max] para su diagrama, entonces en:

• La escala de frecuencia logarítmica, los límites de frecuencia del diagrama están establecidos en [w_min,w_max] y el diagrama muestra dos ramas, una para frecuencias positivas [w_min,w_max] y una para frecuencias negativas [–w_max,–w_min].

• La escala de frecuencia lineal, los límites de frecuencia del diagrama están establecidos en [–w_max,w_max] y el diagrama muestra una única rama con un rango de frecuencia simétrico centrado en un valor de frecuencia de cero.

Especifique frecuencias en unidades de rad/TimeUnit, donde TimeUnit es la propiedad TimeUnit del modelo.

Algoritmos

El software calcula la respuesta en frecuencia de la siguiente forma:

1. Calcule la representación de cero-polo-ganancia (zpk) del sistema dinámico.

2. Evalúe la ganancia y la fase de la respuesta en frecuencia en función de los datos de ceros, polos y ganancia para cada canal de entrada-salida del sistema.

   • En los sistemas de tiempo continuo, la función bodemag evalúa la respuesta en frecuencia en el eje imaginario s = jω y tiene en cuenta solo frecuencias positivas.

   • En los sistemas de tiempo discreto, la función bodemag evalúa la respuesta en frecuencia en el círculo unitario. Para facilitar la interpretación, el comando parametriza la mitad superior del círculo unitario como:

     $$z=e^{j\omega T_s},0\le \omega \le {\omega }_N=\frac{\pi }{T_s},$$

     donde T_s es el tiempo de muestreo y ω_N es la frecuencia Nyquist. A continuación, el software utiliza la frecuencia de tiempo continuo equivalente ω como variable del eje x. Dado que $$H\left(e^{j\omega T_s}\right)$$ es periódico con periodo 2ω_N, la función bodemag representa la respuesta solo hasta la frecuencia Nyquist ω_N. Si sys es un modelo de tiempo discreto con un tiempo de muestreo no especificado, la función bodemag utiliza T_s = 1.

Funcionalidad alternativa

También puede crear una respuesta en frecuencia de solo magnitud utilizando bodeplot. Para ello, establezca la propiedad PhaseVisible del objeto bodeplot en "off".

bp = bodeplot(sys);
bp.PhaseVisible = "off";

Historial de versiones

Introducido en R2012a

Consulte también

bode | bodeplot | freqresp | nichols | nyquist | step

Temas

• Respuestas en el dominio de la frecuencia
• Modelos de sistemas dinámicos