hht
Hilbert-Huang transform
Syntax
Description
hs = hht(IMFs)hs of the signal specified by
intrinsic mode functions IMFs. hs is
useful for analyzing signals that comprise a mixture of signals whose spectral
content changes in time. Use hht to perform Hilbert
spectral analysis on signals to identify localized features.
[___] = hht(___,
estimates Hilbert spectrum parameters with additional options specified by one
or more name-value arguments.Name=Value)
hht(___) with no output arguments plots the
Hilbert spectrum in the current figure window. You can use this syntax with any
of the input arguments in previous syntaxes.
hht(___,
plots the Hilbert spectrum with the optional freqlocation)freqlocation
argument to specify the location of the frequency axis. Frequency is represented
on the y-axis by default.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The Hilbert-Huang transform is useful for performing time-frequency analysis of nonstationary and nonlinear data. The Hilbert-Huang procedure consists of the following steps:
emdorvmddecomposes the data set x into a finite number of intrinsic mode functions.For each intrinsic mode function, xi, the function
hht:Uses
hilbertto compute the analytic signal, , where H{xi} is the Hilbert transform of xi.Expresses zi as , where ai(t) is the instantaneous amplitude and is the instantaneous phase.
Computes the instantaneous energy, , and the instantaneous frequency, . If given a sample rate,
hhtconverts to a frequency in Hz.Outputs the instantaneous energy in
imfinseand the instantaneous frequency inimfinsf.
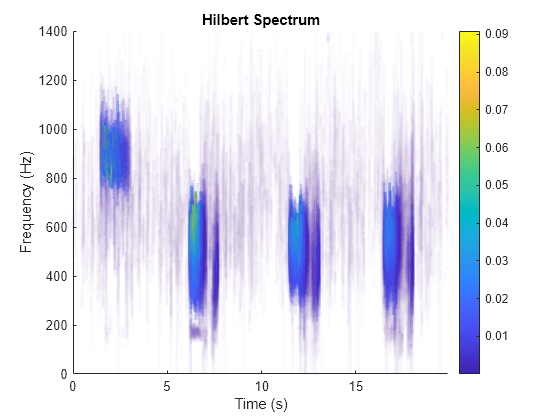
When called with no output arguments,
hhtplots the energy of the signal as a function of time and frequency, with color proportional to amplitude.
References
[1] Huang, Norden E, and Samuel S P Shen. Hilbert–Huang Transform and Its Applications. 2nd ed. Vol. 16. Interdisciplinary Mathematical Sciences. WORLD SCIENTIFIC, 2014. https://doi.org/10.1142/8804.
[2] Huang, Norden E., Zhaohua Wu, Steven R. Long, Kenneth C. Arnold, Xianyao Chen, and Karin Blank. “ON INSTANTANEOUS FREQUENCY.” Advances in Adaptive Data Analysis 01, no. 02 (April 2009): 177–229. https://doi.org/10.1142/S1793536909000096.